
半径 r の円の面積は、πr2 である。また、長軸の長さ、短軸の長さがそれぞれ a 、b で
ある楕円の面積は、 πab である。
a=b のとき、楕円は円となり、 πab=πa2 で、円の面積の公式に一致する。
同様の関係が、直円錐の側面積の場合にも成り立つことを、最近気づいた。
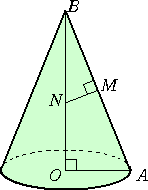
左図のような、底面の半径 OA、高さ OB の直円錐の側面積 S
は、母線の長さ AB を用いて、
S=πOA・AB
で与えられる。
直円錐の高さ OB が潰れたとき、 AB=OB となり、 S=πOA2 で、円の面積の公
式に一致する。
(証明) 側面を展開すると、半径 AB、弧の長さ(=底面の円周の長さ) 2πOA の扇形
なので、その面積は、 (1/2)×(半径)×(弧の長さ) という公式により、
S=(1/2)×AB×2πOA=πOA・AB
となる。 (証終)
さらに、母線 AB の中点 M で垂線を引き、直線 OB との交点を N とおくと、
S=2πOB・MN
が成り立つ。
(証明) △OAB∽△MNB なので、 OA : OB=MN : MB が成り立つ。
よって、 OA・MB=OB・MN である。
2MB=AB なので、 OA・AB=2OB・MN より、
S=2πOB・MN
が成り立つ。 (証終)
(参考文献 : プリトゥロ 著 松田信行 訳 幾何の論証とその指導 (東京図書))
(追記) 令和7年7月11日付け
次の東北大学 後期理系(1996)の問題は、直円すいの側面積に関する問題である。
問題 頂点から底面に下ろした垂線の足が底面の円の中心に一致する円すいを直円すい
と呼ぶ。側面積が6πである直円すいのなかで体積が最大となるものを考える。このとき、
底面の半径および高さを求めよ。
(解) 底面の半径を r 、高さを h 、母線の長さを x 、扇形の中心角をθとおくと、
xθ=2πr 、(1/2)x2θ=6π より、 x・2πr=6π すなわち、 x=6/r
また、 x2=h2+r2 より、 h2=36/r2−r2
直円すいの体積をVとおくと、 V=(1/3)πr2h
y=9V2/π2=r4h2=36r2−r6 とおくと、 y’=72r−6r5=6r(12−r4)=0 から、
r4=12 すなわち、 r=4√12 のとき、yは極大かつ最大となる。
このとき、 h2=36/(2
以下、工事中!