実数の不思議　　　 　　　　　　　　　　　　　　　　　　　戻る

　中学校レベルの数学では、実数そのものを特に意識することはない。せいぜい、循環しない
無限小数の存在に新鮮な驚きを覚えるくらいだ。高校で、微分積分を学ぶとき、否応にも実数
というものの存在に直面せざるをえない。実数の連続性という概念が根底にあるからだ。

　以前の学習指導要領では、現在の現地調達方式のものと違って、高校１年から、チラチラッ
と、有理数と無理数の本質的違いに気づかせる問題が、微分積分を学習するまでの道中に
並べられていた。

　たとえば、『等式　Ｘ＋Ｙ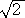＝３　を満たす有理数 Ｘ，Ｙ を求めよ。』などは、無理数を扱う上
での注意点を教えてくれる。

　大学では、実数についての厳密な定義に遭遇する。そこから、真の意味での「数学の研究」
が始まる。Ｄｅｄｅｋｉｎｄ の切断で実数を構成している教科書が多いが、率直なところ、疲れる。

　実は、実数を特徴づけるものとして、いくつか同値なものが知られている。
以下で、Ｎは、自然数の集合で、Ｒ は、実数の集合とする。

（１）・・・Ｄｅｄｅｋｉｎｄ（実数の連続性の公理）
　　　Ａ，Ｂ⊂Ｒ、Ａ≠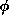　、Ｂ≠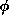　に対して、Ｒ＝Ａ∪Ｂ、Ａ∩Ｂ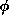＝　であり、さらに
　　　ａ∈Ａ、ｂ∈Ｂ に対して、ａ＜ｂ が成り立つとき、
　　　ｍａｘＡ　または　ｍｉｎＢ　のどちらか一方だけが必ず存在する。

（２）・・・Ｗｅｉｅｒｓｔｒａｓｓ（実数の制限完備性）
　　　Ａ⊂Ｒ、Ａ≠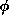　となるＡが上に（下に）有界ならば、ｓｕｐＡ（ｉｎｆＡ）が存在する。

（３） 上に（下に）有界で、単調増加（減少）な数列は収束する。

（４） （イ）任意の正数 ａ、ｂ に対して、ｎａ＞ｂ となる自然数 ｎ が存在する。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（Ａｒｃｈｉｍｅｄｅｓ の原理）
　　　（ロ）任意の ｎ に対して、閉区間 ［ａｎ，ｂｎ］⊂Ｒ で、［ａｎ，ｂｎ］⊃［ａｎ+1，ｂｎ+1］ のとき、
　　　　　　∩［ａｎ，ｂｎ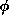］≠　である。（Ｃａｎｔｏｒ の共通部分定理）

（５）・・・Ｈｅｉｎｅ‐Ｂｏｒｅｌ の被覆定理
　　　開区間 Ｕ の集合族により、閉区間 ［ａ，ｂ］ が被覆されているとき、有限個の開区間を
　　　選んで、［ａ，ｂ］⊂Ｕ1∪Ｕ2∪・・・∪Ｕn　とできる。

（６）・・・Ｂｏｌｚａｎｏ‐Ｗｅｉｅｒｓｔｒａｓｓ の定理）
　　　Ｒの任意の有界な無限集合は、少なくとも１つの集積点をもつ。

（７） 有界数列は収束する部分列をもつ。

（８） （イ）任意の正数 ａ、ｂ に対して、ｎａ＞ｂ となる自然数 ｎ が存在する。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（Ａｒｃｈｉｍｅｄｅｓ の原理）
　　　（ロ）任意のＣａｕｃｈｙ列は収束する。（Ｃａｕｃｈｙ の定理・・・実数の完備性）

　上記の実数の性質の中で、私にとって一番感動的なのは、Ａｒｃｈｉｍｅｄｅｓ の原理である。
ａ がどんなに小さくても、ｂ がどんなに大きくても、小さい ａ を懸命に繰り返し加えれば、つい
には、ｂ を追い越してしまうというところに、数学版「うさぎとかめ」の物語を思い浮かべる。
あるいは、「塵も積もれば山となる」と思ってもよい。

　しかも、この当たり前のような性質が、上からも分かるように、実数を規定する性質として、
本質的なものであることに驚かされる。

また、このＡｒｃｈｉｍｅｄｅｓ の原理は、極限計算の基本公式： 　と同値である。

（証明）　任意のε＞０ に対して、Ａｒｃｈｉｍｅｄｅｓ の原理より、Ｎε＞１となる自然数Ｎが存在
　　　　　する。このとき、ｎ＞Ｎ　ならば、０＜１/ｎ＜１/Ｎ＜ε　なので、明らかである。
　　　　　逆に、ａ/ｂ に対して、ある自然数Ｎが存在して、ｎ＞Ｎ　ならば、１/ｎ＜ａ/ｂ　なので
　　　　　明らかである。

　Ａｒｃｈｉｍｅｄｅｓ の原理を用いると、いろいろ面白い性質を導くことが出来る。

（性質１）　任意の実数 Ｘ に対して、ｎ−１≦Ｘ＜ｎ　となる整数 ｎ が存在する。

　これは、隣り合う整数同士の距離が１なので、直感的に正しいと理解されると思うが、厳密
には次のように示される。

　　　　　（証明）　Ｘ＝０　ならば、ｎ＝１
　　　　　　　　　　 Ｘ＞０　ならば、Ａｒｃｈｉｍｅｄｅｓ の原理より、Ｘ＜ｍ・１＝ｍ　となる自然数 ｍ
　　　　　　　　　　が存在する。このような ｍ のうちで最小値を ｎ とすればよい。
　　　　　　　　　　Ｘ＜０　ならば、ｍ−１≦−Ｘ＜ｍ　となる自然数 ｍ が存在するので、
　　　　　　　　　　−ｍ＜Ｘ≦−ｍ＋１　となる。そこで、ｎ＝−ｍ　または　ｎ＝−ｍ＋１とおけ
　　　　　　　　　　ばよい。

（性質２）　実数の任意の開区間は、必ず有理数を含む。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　
　これは、「有理数 ａ、ｂ　（ａ＜ｂ）に対して、（ａ＋ｂ）/２ は有理数で、ａ　と ｂ の間にある」と
いう有理数の稠密性を実数の場合に拡張したものだが、次のように示される。

　　　　　（証明）　いま、実数の任意の開区間として、ａ＜Ｘ＜ｂ　とする。
　　　　　　　　　　Ａｒｃｈｉｍｅｄｅｓ の原理より、ｍ(ｂ−ａ)＞１　となる自然数 ｍ が存在する。
　　　　　　　　　　このとき、（性質１）により、ｎ−１≦ｍａ＜ｎ　となる自然数 ｎ が存在する。
　　　　　　　　　　よって、ａ＜ｎ/ｍ≦ａ＋１/ｍ＜ｂ　が成り立ち、有理数 ｎ/ｍ が存在する。

（性質２）から、どんな実数のどんな近くにも有理数があるわけで、実数の濃度と有理数の
濃度の違いを思うと、とても不思議な感じがする。

　さらに、無理数についても、同様なことがいえる。

（性質３）　実数の任意の開区間は、必ず無理数を含む。

　　　　　（証明）　いま、実数の任意の開区間として、ａ＜Ｘ＜ｂ　とし、Ｘはすべて有理数と
　　　　　　　　　仮定する。（性質２）から、ａ＜ｐ＜ｑ＜ｂ　となる有理数 ｐ、ｑ が存在する。
　　　　　　　　　よって、ｒ＝ｑ−ｐ　も有理数である。任意の無理数Ｍに対して、（性質１）か
　　　　　　　　　ら、ｎ−１≦（Ｍ−ｐ）/ｒ＜ｎ　となる整数 ｎ が存在する。このとき、
　　　　　　　　　ｐ≦Ｍ−ｒ（ｎ−１）＜ｐ＋ｒ＝ｑ　より、Ｍ−ｒ（ｎ−１）　すなわち　Ｍ が有理数
　　　　　　　　　となり、これは矛盾する。よって、必ず無理数を含む。

　このように、Ａｒｃｈｉｍｅｄｅｓ の原理は、実数の集合にとって有用な定理ではあるが、実は、
当たり前の性質ではないことを肝に銘じておかなければならない。

Ａｒｃｈｉｍｅｄｅｓ の原理が成り立たない例

　集合 Ｓ＝Ｚ4＝｛０，１，２，３｝　（整数を４で割った余りの集合）において、演算◎を
Ｘ、Ｙ∈Ｓ　に対して、Ｘ＋Ｙ の値を ４ で割った余り Ｒ を用いて、Ｘ◎Ｙ＝Ｒ　と定義する。
Ｘ◎Ｘ＝２・Ｘ、Ｘ◎２Ｘ＝３・Ｘ、．．．とし、一般に、自然数 ｎ に対して、ｎ・Ｘ＝Ｘ◎（ｎ−１）Ｘ　
により、ｎ・Ｘ を定義する。
このとき、任意の自然数 ｎ に対して、ｎ・２＜３　が成り立ち、Ａｒｃｈｉｍｅｄｅｓ の原理は成り
立たない。

（参考文献：菅原正博　著　位相への入門（朝倉書店）
　　　　　　　 石谷　茂　著　トポロジー入門（現代数学社））