おみくじの数理　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

　おみくじの数理というと、「大吉」や「中吉」、「小吉」、「末吉」はたまた「大凶」などの出現
する割合の話かと想像されるかもしれないが、このページで取り上げるのは、

　　「おみくじを綺麗に折ると、正５角形ができる」

というものである。

　この事実は昔から有名で、実際に折ってみると確かに正５角形っぽくなる。これまで、そ
のことを証明しようと思わなかったが、「正５角形っぽい」という表現が嫌いなので、証明し
てみようと思い立った次第である。

　神社のおみくじのサイズは全て約２３．５ｃｍ×約５．８ｃｍと決まっているらしい。長形３号
封筒のサイズが２３．５ｃｍ×１２．０ｃｍなので、だいたいその半分ぐらいの大きさだ。

　神社のおみくじ売り場の近くには大抵木が植えられていて、その木におみくじを結ぶよう
になっている。（もしかしたら参拝者が勝手に使用済みのおみくじを結んでいるだけかも？）

　いま、おみくじを長辺に平行に折って、下図のような長方形ができたとしよう。

　　

　次のように折って、結び目を作る。

　　　　　　　　　　　　

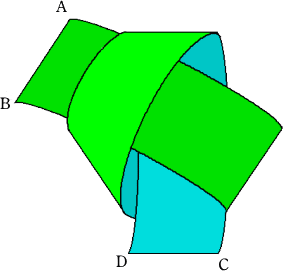
　このとき、結び目がちょうど「正５角形」になっているというわけである。

　　　　

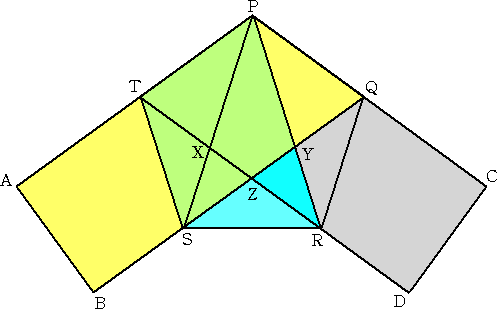
　このことを証明するには、次の性質（※）が基本である。

　長方形を線分ＭＮで折り曲げるとき、　∠ＢＮＭ＝∠ＤＭＮ　である。



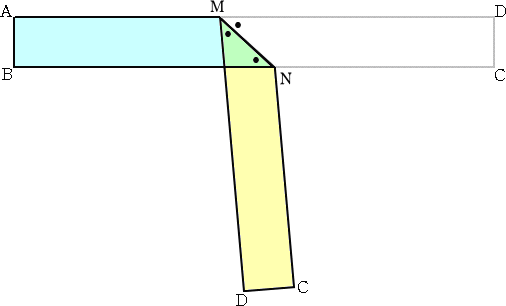
　上図で、∠ＢＮＭと∠ＤＭＮは平行線の錯角なので等しいことは明らかだろう。

　さて、本題の証明に取りかかろう。

（証明）　折り方の対称性から、ＰＱ＝ＰＴ　としてよい。このとき、性質（※）より、

	△ＰＱＳ、△ＰＴＲ、△ＰＳＲは 二等辺三角形である。 　　ＰＳ＝ＱＳ　、　ＰＳ＝ＰＲ　、 　　ＰＲ＝ＴＲ 　が成り立つので、 　　ＰＳ＝ＱＳ＝ＰＲ＝ＴＲ 　よって、 　　△ＰＳＱ≡△ＴＲＰ 　そこで、∠ＰＳＱ＝・　とすると、
∠ＴＲＰ＝・　となる。　このとき、平行線の錯角は等しいので、 　　∠ＰＳＱ＝∠ＴＲＰ＝∠ＳＰＴ＝∠ＳＴＲ＝∠ＳＱＲ＝∠ＱＰＲ＝・　となる。 　また、ＰＱとＴＲは平行なので、∠ＰＱＳ＝∠ＴＺＳ 　よって、　△ＰＱＳ∽△ＳＺＴ　となり、　∠ＺＳＴ＝∠ＱＰＳ 　∠ＰＱＳ＝∠ＱＰＳ　なので、　∠ＰＱＳ＝∠ＺＳＴ　より、四角形ＰＱＳＴは等脚台形となる。 　よって、　ＰＱ＝ＴＳ　が成り立つ。　このとき、　ＰＴ＝ＴＳ　となり、△ＰＴＳは二等辺三角形。 　このことから、　∠ＰＳＴ＝∠ＳＰＴ＝・　となる。 　平行線の錯角は等しいので、　∠ＰＳＴ＝∠ＳＰＲ＝∠ＰＲＱ＝・　となる。（上図参照） 　したがって、　５角形ＰＱＲＳＴの内角がすべて等しくかつ５辺の長さもすべて等しくなるので、 正５角形と言える。　（証終）

（コメント）　この話題は、当ＨＰがいつもお世話になっている、らすかるさんが他所のＨＰで考
　　　　　　えられていたものを参考にさせていただいた。らすかるさんに感謝いたします。