嵟戝偺惓嶰妏宍 丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
丂侾曈偺挿偝偑俇偺惓嶰妏宍俙俛俠偵奜愙偡傞惓嶰妏宍俢俤俥傪峫偊傞丅
丂丂丂丂丂丂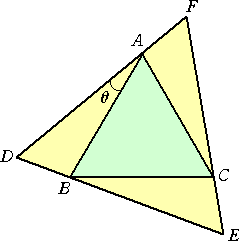
丂惓嶰妏宍俢俤俥偺柺愊偑嵟戝偵側傞偲偒丄妏兤偼壗搙偩傠偆偐丠丂偙傟偼拞妛惗儗儀儖偺
庤崰側弶摍婔壗偺栤戣偩傠偆丅
丂丂丂丂丂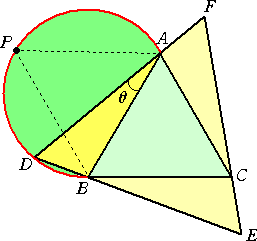
丂忋恾偺傛偆偵尫俙俛偵懳偡傞墌廃妏偼忢偵堦掕乮俇侽搙乯偱偁傞偺偱丄揰俢偼墌廃忋傪摦偔丅
仮俙俛俢偺柺愊偑嵟戝偵側傞偺偼丄俹俙亖俹俛丂偺応崌偱偁傞丅傛偭偰丄仮俙俛俹偼惓嶰妏宍
偲側傝丄兤亖俇侽亱偱偁傞丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂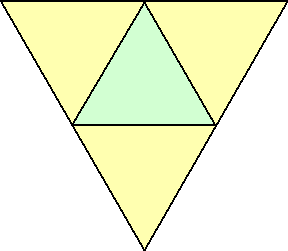
丂忋婰偺峫偊曽偼丄悢妛嘦偺乽恾宍偲曽掱幃乿傗悢妛俙偺乽暯柺婔壗乿偱傕妛傇丅
丂偙偺応崌丄仮俙俛俢偺傒傪峫偊丄懠傪峫偊偰偄側偄偺偼丄仮俙俛俠偑惓嶰妏宍偲偄偆摿庩側
応崌備偊嫋偝傟傞偙偲偱偁傞丅
丂偙偙偱丄仮俙俛俠偑傛傝堦斒揑側応崌偵旛偊偰丄偦傟偵尒偁偭偨夝朄傪帵偟偰偍偙偆丅
 |
丂嵍恾偵偍偄偰丄丂佢俛俙俢亖兤丄佢俙俢俛亖俇侽亱偐傜
佢俙俛俢亖侾俀侽亱亅兤丂偲側傞丅
丂傛偭偰丄仮俙俛俢偵偍偄偰丄惓尫掕棟偵傛傝丄
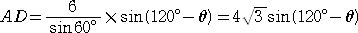
偲側傞丅
丂摨條偵偟偰丄佢俙俠俥亖兤丂偱偁傞偺偱丄
丂丂丂丂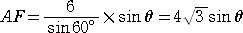 |
丂傛偭偰丄
俢俥亖係 乮倱倝値兤亄倱倝値乮120亱亅兤乯乯亖係
乮倱倝値兤亄倱倝値乮120亱亅兤乯乯亖係 亊俀倱倝値60亱們倧倱乮兤亅60亱乯亖侾俀們倧倱乮兤亅60亱乯
亊俀倱倝値60亱們倧倱乮兤亅60亱乯亖侾俀們倧倱乮兤亅60亱乯
0亱亝兤亝180亱偱偁傞偺偱丄俢俥偼丄兤亅60亱亖0亱丂懄偪丄兤亖俇侽亱偺偲偒丄嵟戝偲側傞丅
偙偺偲偒丄仮俢俤俥偺柺愊傕嵟戝偲側傞丅
丂撉幰偺偨傔偵丄楙廗栤戣傪巆偟偰偍偙偆丅
栤戣丂丂捀妏偑俁侽亱偺俀摍曈嶰妏宍偵奜愙偡傞惓嶰妏宍偺偆偪柺愊偑嵟戝偲側傞偲偒偺侾曈偺
丂丂丂丂挿偝傪媮傔傛丅偨偩偟丄摍曈偺挿偝偼丄俇偲偡傞丅
丂摎偊偼丄丂係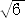 丂丅丂奆偝傫丄偱偒傑偟偨偐丠
丂丅丂奆偝傫丄偱偒傑偟偨偐丠



