
丂丂 幚 椡 僥 僗 僩丂丂丂丂丂丂丂丂丂 丂丂丂丂丂丂丂巵柤丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂.
嘥丏丂倶 偺惍幃 倶値乮倶2亄倎倶亄倐乯 傪乮倶亅俀乯2偱妱偭偨偲偒偺梋傝偑 俀値乮倶亅俀乯偲側傞偲偒丄掕
丂丂悢 倎丄倐 偺抣傪媮傔傛丅
嘦丏丂嬻娫偵偍偄偰丄師偺栤偄偵摎偊傛丅
丂乮侾乯丂俁揰俙乮俁丆侾丆俀乯丄俛乮係丆俆丆係乯丄俠乮俈丆俁丆侾侽乯偲偡傞丅俛俠忋偺揰俢偵偮偄偰丄俙俢偑
丂丂丂佢俛俙俠偺俀摍暘慄偱偁傞偲偒丄揰俢偺嵗昗傪媮傔傛丅
丂乮俀乯丂俀揰俙乮亅俀丆俀丆侾乯丄俛乮俁丆俀丆侾乯偲 倶 幉忋傪摦偔揰俹偑偁傞丅偙偺偲偒丄俹俙亄俹俛偑
丂丂丂嵟彫偲側傞傛偆側揰俹偺嵗昗傪媮傔傛丅
丂乮俁乯丂係揰俷乮侽丆侽丆侽乯丄俙乮侾丆侽丆侽乯丄俛乮侽丆侾丆侽乯丄俠乮亅侾丆侾丆侾乯傪捠傞媴柺偺拞怱傪俹
丂丂丂偲偡傞丅偙偺偲偒丄仮俙俠俹偺柺愊傪媮傔傛丅
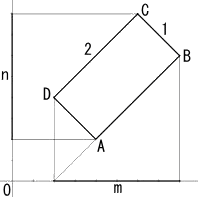
嘨丏丂壓恾偺傛偆偵侾曈偺挿偝俀偺棫曽懱俙俛俠俢-俹俻俼俽偑偁傞丅偄傑丄摦揰俵偑俙偐傜弌敪
丂丂偟偰丄係曈俙俛丄俛俠丄俠俢丄俢俙忋傪俙仺俛仺俠仺俢仺俙偺弴偱侾廃偡傞丅摦揰俵偐傜捈慄俙俻
丂丂偵壓偟偨悅慄偺挿偝偺暯曽傪 倷 丄俙偐傜應偭偨摦揰俵偺摦偄偨嫍棧傪 倶 偲偡傞丅
丂丂丂丂丂丂

丂丂丂偙偺偲偒丄師偺栤偄偵摎偊傛丅
丂乮侾乯丂摦揰俵偑俙俛忋乮侽亝倶亝俀乯偵偁傞偲偒丄y 傪 倶 偺娭悢偲偟偰昞偣丅
丂乮俀乯丂侾廃偡傞偲偒偺 倷 傪 倶 偺娭悢偲偟偰昞偟丄偦偺僌儔僼傪偐偗丅偨偩偟丄侽亝倶亝俉偲偡傞丅
嘩丏丂値傪俀寘偺帺慠悢偲偟丄値傪俆偱妱偭偨偲偒偺彜傪倠偲偡傞丅
丂乮侾乯丂俆偱妱偭偰侾梋傞帺慠悢値偺憤榓傪媮傔傛丅
丂乮俀乯丂値2偑俆偱妱偭偰侾梋傞偲偒丄偦偺傛偆側帺慠悢値偺憤榓傪媮傔傛丅
丂乮俁乯丂値4偑俆偱妱偭偰侾梋傞偲偒丄偦偺傛偆側帺慠悢値偺憤榓傪媮傔傛丅
嘪丏丂嵗昗暯柺忋偺挿曽宍俙俛俠俢偱丄俀曈偺挿偝偑侾偲俀偺傕偺傪峫偊傞丅偙偺傛偆側挿曽宍
丂丂偺倶幉傊偺惓幩塭偺挿偝傪倣丄倷幉傊偺惓幩塭偺挿偝傪値偲偡傞丅壓恾偱丄曈俙俛偺墑挿偲
丂丂倶幉偺側偡妏傪兤偲偡傞丅扐偟丄侽亱亝兤亝俋侽亱丅
丂丂丂丂
丂丂偙偺偲偒丄師偺栤偄偵摎偊傛丅
丂乮侾乯丂倣丄値傪兤偱昞偣丅
丂乮俀乯丂揰乮倣亅値丆倣亄値乯偺慡懱偼丄偳傫側恾宍傪昤偔偐丅
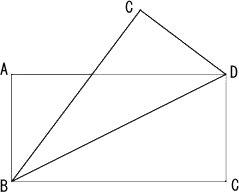
嘫丏丂挿曽宍俙俛俠俢偑偁傞丅扐偟丄俙俛亖俁丄俛俠亖係偲偡傞丅偙偺偲偒丄師偺栤偄偵摎偊傛丅
丂乮侾乯丂懳妏慄俛俢傪愜傝栚偲偟偰丄偙偺挿曽宍傪愜傝嬋偘傞偲偒丄俙俠娫偺嫍棧傪媮傔傛丅
丂丂丂丂
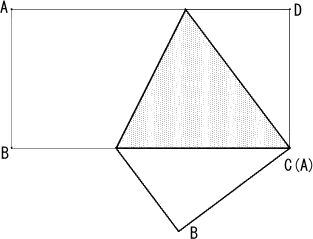
丂乮俀乯丂捀揰俙偲捀揰俠偲偑廳側傞傛偆偵偙偺挿曽宍傪愜傝嬋偘傞丅偙偺偲偒丄愜傝栚偺挿偝偲
丂丂丂丂丄偙偺挿曽宍偑愜傝廳側偭偰偱偒傞嶰妏宍偺柺愊傪媮傔傛丅
丂丂丂丂
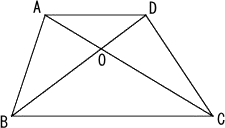
嘮丏丂戜宍俙俛俠俢偵偍偄偰丄俙俢偲俛俠偼暯峴偲偡傞丅懳妏慄俙俠丄俛俢偺岎揰傪俷偲偡傞偲偒丄
丂丂仮俷俙俛偺柺愊偑俀丄仮俷俛俠偺柺愊偑係偱偁傞丅
丂乮侾乯丂俙俢丗俛俠傪媮傔傛丅
丂乮俀乯丂戜宍俙俛俠俢偺柺愊傪媮傔傛丅
丂丂丂丂
嘯丏丂娭悢 倷亖倎倶亄倐 偼丄倶亖侾偺偲偒丄侾亝倷亝俀丄倶亖俀偺偲偒丄俀亝倷亝係偲側傞丅偙偺偲偒丄
丂丂師偺栤偄偵摎偊傛丅
丂乮侾乯丂倶亖俁偺偲偒丄倷偺偲傝偆傞抣偺斖埻傪媮傔傛丅
丂乮俀乯丂倶亖倫偺偲偒丄亅俆亝倷亝倠偲側偭偨丅偙偺偲偒偺倫丄倠偺抣傪媮傔傛丅
佱夝丂摎佲丂奺帺偱嵦揰偺屻丄嵦揰寢壥偺恌抐傪偛棗偔偩偝偄丅
嘥丏丂倎亖亅俁丄倐亖俀丂乮俆揰亊俀亖侾侽揰乯
嘦丏乮侾乯丂俢乮俆丆侾俁/俁丆俇乯丂乮俀乯丂乮侾/俀丆侽丆侽乯丂乮俁乯丂併俁侽/係丂乮俆揰亊俁亖侾俆揰乯
嘨丏乮侾乯丂倷亖乮侾/俀乯倶2丂乮俀乯丂俀亝倶亝係偺偲偒丄丂倷亖乮倶亅俀乯2亄俀丂丄係亝倶亝俇偺偲偒丄丂
丂丂丂丂丂倷亖乮侾/俀乯乮倶亅俇乯2亄係丂丄俇亝倶亝俉偺偲偒丄丂倷亖乮倶亅俉乯2丂乮俆揰亊俀亖侾侽揰乯
丂丂丂丂丂
嘩丏乮侾乯丂俋俇俁丂乮俀乯丂侾俋俉侽丂乮俁乯丂俁俋俇侽丂乮俆揰亊俁亖侾俆揰乯
嘪丏乮侾乯丂倣亖俀們倧倱兤亄倱倝値兤丄値亖俀倱倝値兤亄們倧倱兤
丂丂乮俀乯丂倶2/俀亄倷2/侾俉亖侾丂乮俁亝倷亝俁
嘫丏乮侾乯丂俈/俆丂乮俀乯丂愜傝栚偺挿偝偼丄侾俆/係丄柺愊偼丄俈俆/侾俇丂丂乮俆揰亊俁亖侾俆揰乯
嘮丏乮侾乯丂俙俢丗俛俠亖侾丗俀丂乮俀乯丂柺愊偼丄俋丂丂乮俆揰亊俀亖侾侽揰乯
嘯丏乮侾乯丂俀亝倷亝俈丂乮俀乯丂倫亖皞P丄倠亖俀丂丂乮俆揰亊俁亖侾俆揰乯
丂丂丒丒丒丒丒丒丒丒丒丒丒丒丒丒丂偁側偨偺揰悢偼丄乮丂丂丂丂丂丂丂丂乯揰
丂幚椡僥僗僩偺恌抐寢壥