
当HPがいつもお世話になっているHN「よおすけ」さんからの出題です。
(令和4年4月1日付け)
6辺の長さ、体積がともに整数の四面体ABCDがある。
AB=31、BC=33、AC=34、CD=35、BD=32 のとき、ADを答えよ。
(答え) AD=11のとき、体積は1680 、AD=53のとき、体積は3024
実際に、
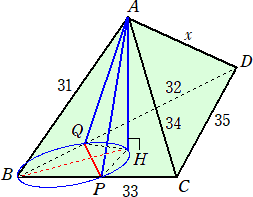
頂点Aより、底面BCDに垂線を下ろし、その足をHとする。また、Aより辺BC、BDに垂線
を下ろし、その足をそれぞれP、Qとする。また、AD=x とおく。
三垂線の定理から、HP⊥BC、HQ⊥BD なので、4点B、P、H、Qは同一円周上にあり、
BHはその直径となる。
ヘロンの公式を用いて、 (33+35+32)/2=50 から、
△BCD=√(50・17・15・18)=30√255
余弦定理から、 cos∠ABC=149/341 、cos∠CBD=37/88
cos∠ABD=(1985−x2)/1984
よって、 BP=149/11 、 BQ=(1985−x2)/64 である。
余弦定理より、PQが求められ、また、正弦定理より、BH=PQ/sin∠CBD も求められる。
よって、 AH2=AB2−BH2 から、四面体の高さAHが求められるので、AHと△BCDか
ら、四面体の体積 (1/3)AH・△BCD が求められる。
#途中の計算が膨大で、何とか数式をまとめて、最後は、Excel 先生の助っ人を得て、答え
が得られました。皆さんは、どう解かれますか?もっと計算量の少ないエレガントな解答は
ないものでしょうか? もし、ありましたら、是非、ご教示ください。
(参考) 次は、x=11のときの計算過程です。
BP=149/11 、 BQ=233/8
cos∠ABC=149/341 、cos∠CBD=37/88 、cos∠ABD=233/248
これより、 PQ2=5420775/7744 なので、 BH2=72277/85
よって、 AH2=9408/85 から、 AH=(56/85)√255
以上から、四面体の体積は、 (1/3)・(56/85)√255・30√255=1680 となり、
確かに整数である。
同様に、x=53のときも計算しておこう。
cos∠ABC=149/341 、cos∠CBD=37/88 、cos∠ABD=−103/248 で、
∠ABDは鈍角である。
BP=149/11 、 BQ=103/8 で、QはDBの延長上にあるので、
PQ2=BP2+BQ2−2BP・BQ・cos(π−∠CBD)=3840231/7744
よって、BH2=1280077/2125 より、 AH2=762048/2125 から、
AH=1512/√6375 となる。
以上から、四面体の体積は、 (1/3)・1512/√6375・30√255=3024 となり、
確かに整数である。
以下、工事中!