ベクトルと正三角形　 　　　　　　　　　 　　　　　　　　　　　　　　　

　当ＨＰがいつもお世話になっているＨＮ「よおすけ」さんからの出題です。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（令和２年６月１６日付け）

　正三角形ABCがある。点Oを直線ABに関してCと反対側にとって、∠AOB=60°となるよう
にし、ベクトルOA、OB、OCをそれぞれa、b、cで表す。

　このとき、　c＝{|b|/|a|}a＋{|a|/|b|}b　であることを証明せよ。

（出典）:京都大学前期理系（1973）



































（答え）　Ｏ（０，０）、Ａ（２ａ，０）、Ｂ（２ｂ，２ｂ）とおく。

　このとき、　ＡＢ＝（２ｂ−２ａ，２ｂ）　で、点Ａの周りに−６０°回転させると、

　ＡＣ＝（４ｂ−ａ，ａ）　なので、　Ｃ（ａ＋４ｂ，ａ）

　そこで、　ｃ＝ｍａ＋ｎｂ　とおくと、a、b は互いに一次独立で、

　　　２ａｍ＋２ｂｎ＝ａ＋４ｂ　、２√３ｎｂ＝ａ

　これらを解いて、　ｎ＝ａ/（２ｂ）　、ｍ＝２ｂ/ａ

　ここで、　|a|＝２ａ、|b|＝４ｂ　なので、　ｎ＝|a|/|b|　、ｍ＝|b|/|a|

　よって、　ｃ＝（|b|/|a|）ａ＋（|a|/|b|）ｂ　　（終）


　Ｓ（Ｈ）さんからのコメントです。（令和２年６月１６日付け）

　都合上添字を付けて、　A₁=（0，1）、B₁=（-/2)，-1/2）、C₁=（/2，-1/2）とすると、
問のOは、　O₁=（-，1）　で、四角形O₁B₁C₁A₁はひし形となり、

　C₁-O₁=(A₁-O₁)+(B₁-O₁) 　すなわち、　ｃ＝ａ＋ｂ

　ここで、　|a|＝|b|＝　なので、　ｃ＝（|b|/|a|）ａ＋（|a|/|b|）ｂ　が言える。（Q.E.D.）


（コメント）　特殊な場合に限定しての（Q.E.D.）ですね。


　ＰＢさんからのコメントです。（令和２年６月１９日付け）

　次のような別解を考えました。

　直線ABに関して、Cと対称な点Dをとる。△ABDは△ABCと合同な正三角形であり、OとD
が一致するとき、|a|＝|b|より与式は成り立つ。（←　Ｓ（Ｈ）さんの解答と同趣旨）

　よって、Oは直線BDに関してAと反対側にあるとして一般性を失わない。

　　

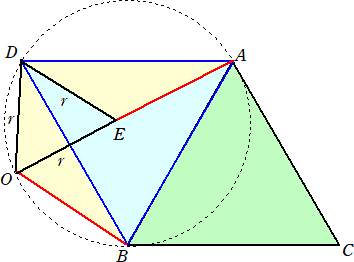
　四角形ADOBは円に内接し、AO上にEO=DO（＝ｒ とする）となる点Eを取れば、△EDOも正
三角形であるから、　△EAD≡△OBD

　よって、　AE＝BO　なので、　ｒ＝|a|−|b|　が成り立つ．

さらに、a、b と平行な単位ベクトル｛1/|a|｝a、｛1/|b|｝b を用いて、

　OD＝OE+ED＝｛ｒ/|a|｝a−｛ｒ/|b|｝b　であるから

ｃ＝OD＋（DA＋DB）＝OD＋（OA−OD）＋（OB−OD）＝OA＋OB−OD
　＝a＋ｂ−｛ｒ/|a|｝a＋｛ｒ/|b|｝b＝｛1−ｒ/|a|｝a＋｛1＋ｒ/|b|｝b＝｛|b|/|a|｝a＋｛|a|/|b|｝b

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　(証明終)

（コメント）　ＰＢさん、いつも斬新な解答ありがとうございます。