２等辺三角形２ 　 　　　　 　　　　　　　　 　　　　　　　　　　　　　　　戻る

　当ＨＰがいつもお世話になっているＨＮ「よおすけ」さんからの出題です。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（平成２８年１月２４日付け）

　頂角が３６°、底辺が２の二等辺三角形を用いて、cos１０８°の値を求めなさい。







































（答）　下図のような図形において、

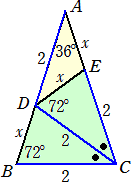　　△ＡＢＣ∽△ＣＤＥ　より、　ｘ＋２ ： ２＝２ ： ｘ

　よって、　ｘ2＋２ｘ−４＝０　を解いて、ｘ＝−１

　　△ＡＤＣにおいて、∠ＡＤＣ＝１０８°で、余弦定理より、

　ｃｏｓ１０８°＝｛４＋４−（＋１）2｝/８＝（１−）/４

＃　３６°が絡む図形の問題は、時には正５角形の性質とも関係してきて、世の中には種々
　の良問が存在している。次の岩手大学の問題が有名でしょう。

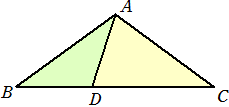
問題　AB=AC=1の二等辺三角形ABCにおいて、辺BC上の点Dが条件：DA=DB、CA=CD を
　　　満たしている。このとき、次の問いに答えよ。

(１)　△ABC∽△DAB であることを用いて、BDの長さを求めよ。
(２)　∠B を求めよ。
(３)　ｃｏｓ∠B を求めよ。

　　　

　問題の条件から、この問題が正５角形の問題と気づいた受験生は果たして何人いただろ
うか？

（解）（１）　DA=DB=ｘ　とおくと、△ABC∽△DAB より、　ｘ ： １=１ ： ｘ+１

　　　　　よって、　ｘ2＋ｘ−1=0　　これを解いて、　ｘ＝(−1+√5)/2

　　　　　すなわち、　BD＝(−1+√5)/2

（２）　∠B=θとおくと、∠ＢＡＤ=θで、∠ＡＤＢ=2θ、∠ＤＡＢ=2θ、∠Ｃ=θ

　　　よって、　5θ=180°より、　θ=36°　すなわち、∠B=36°

（３）　△ＡＢＣにおいて、余弦定理より、

　　　ｃｏｓ∠B=［1+｛(1+√5)/2｝2-1］/(1+√5)=(1+√5)/4　　（終）


（コメント）　（２）から、3θ=180°−2θとして、３倍角の定理、２倍角の定理を活用する解法
　　　　　　もあるが、図形の性質を用いた方が計算は容易である。