
 左図のように、正三角形の頂点と各辺の中点にそれ
左図のように、正三角形の頂点と各辺の中点にそれぞれ円が描かれている。
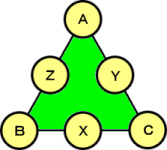
第一問 6個の円上に相異なる整数を配置して、し
かも、各辺の3つの整数の積が、いずれも
2004 になるようにしたい。
どうすればよいか?
第二問 6個の円上に、1から6までの整数をすべ
て配置して、しかも、各辺の3つの整数の和
が、いずれも等しくなるようにしたい。
どうすればよいか?
(第一問の答) 2004=22×3×167 と素因数分解できるので、これら素因数を適当に
分散させて配置すればよい。
魔のトライアングル 
 左図のように、正三角形の頂点と各辺の中点にそれ
左図のように、正三角形の頂点と各辺の中点にそれ
ぞれ円が描かれている。
第一問 6個の円上に相異なる整数を配置して、し
かも、各辺の3つの整数の積が、いずれも
2004 になるようにしたい。
どうすればよいか?
第二問 6個の円上に、1から6までの整数をすべ
て配置して、しかも、各辺の3つの整数の和
が、いずれも等しくなるようにしたい。
どうすればよいか?
(第一問の答) 2004=22×3×167 と素因数分解できるので、これら素因数を適当に
分散させて配置すればよい。
 |
解は、回転と対称性を無視して、次の 11 通り。 |
| A=1 、B=2 、C=3 、X=2×167=334 、 Y=22×167=668 、Z=2×3×167=1002 |
|
| A=1 、B=2 、C=2×3=6 、X=167 、 Y=2×167=334 、Z=2×3×167=1002 |
|
| A=1 、B=2 、C=167 、X=2×3=6 、 Y=22×3=12 、Z=2×3×167=1002 |
|
| A=1 、B=2 、C=2×167=334 、X=3 、 Y=2×3=6 、Z=2×3×167=1002 |
|
| A=1 、B=3 、C=22=4 、X=167 、 Y=3×167=501 、Z=22×167=668 |
|
| A=1 、B=3 、C=167 、X=22=4 、 Y=22×3=12 、Z=22×167=668 |
|
| A=1 、B=3 、C=2×167=334 、X=2 、 Y=2×3=6 、Z=22×167=668 |
|
| A=1 、B=22=4 、C=167 、X=3 、 Y=22×3=12 、Z=3×167=501 |
|
| A=1 、B=2×3=6 、C=167 、X=2 、 Y=22×3=12 、Z=2×167=334 |
|
| A=2 、B=3 、C=167 、X=22=4 、 Y=2×3=6 、Z=2×167=334 |
|
| A=2 、B=2×3=6 、C=2×167=334 、 X=1 、Y=3 、Z=167 |
(第二問の答)
 一つの辺上の3つの整数の和をWとおくと、条件より、
一つの辺上の3つの整数の和をWとおくと、条件より、
A+B+C=3(W−7)
が成り立つ。 6≦A+B+C≦15 なので、9≦W≦12
よって、W=9、10、11、12 の場合について調べれば
よい。
W=9 のとき、
A+B+C=6 なので、A=1 、B=2 、C=3 で、X=4 、Y=5 、Z=6
W=10 のとき、
A+B+C=9 なので、A=1 、B=3 、C=5 で、X=2 、Y=4 、Z=6
(A,B,C)=(1,2,6)、(2,3,4) の場合は不適。
W=11 のとき、
A+B+C=12 なので、A=2 、B=4 、C=6 で、X=1 、Y=3 、Z=5
(A,B,C)=(1,5,6)、(3,4,5) の場合は不適。
W=12 のとき、
A+B+C=15 なので、A=4 、B=5 、C=6 で、X=1 、Y=2 、Z=3