
当HPがいつもお世話になっているHN「よおすけ」さんからの出題です。
(令和4年1月1日付け)
∠A=7π/9、∠B=∠C=π/9、AB=CA=1の二等辺三角形がある。
この三角形を使って、cos(π/9)cos(2π/9)cos(4π/9)の値を既約分数で表せ。
(答) 2等辺三角形を用いなくとも、次のように計算できますね。
P=cos(π/9)cos(2π/9)cos(4π/9) とおくと、
P・8sin(π/9)
=4sin(2π/9)cos(2π/9)cos(4π/9)=2sin(4π/9)cos(4π/9)=sin(8π/9)
ここで、 sin(π/9)=sin(8π/9)≠0 なので、 P・8=1 より、 P=1/8
これに対して、「2等辺三角形を使って」という条件が付いているので、次のように解いて
みました。
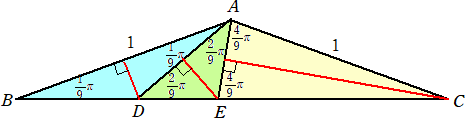
上図より、 AE=2cos(4π/9) 、AD=2AEcos(2π/9) 、AB=2ADcos(π/9) なので、
2[2{2cos(4π/9)}cos(2π/9)]cos(π/9)=8cos(π/9)cos(2π/9)cos(4π/9)=1
よって、 cos(π/9)cos(2π/9)cos(4π/9)=1/8