
当HPがいつもお世話になっているHN「GAI」さんからの出題です。(平成21年12月19日)
ある点から東西南北いずれの方向でもいいから、1進む。そこで直角に曲がり、2進む。さ
らに、そこで直角に曲がり、3進む。
これを繰り返していき、直角に曲がってから、4、5、6、7 の距離進んでいき、最後8の距
離進んだ時に元の出発点に戻るコースどり(前のコースは横切らないこと。)のパターンを調
べて下さい。(これを、位数8の散歩コースと呼ぶことにします。)
同じく、位数16の散歩コース、位数24の散歩コースでは何種類が可能かを調べて下さい。
何方か挑戦して頂けませんか?
(答) まだ、解答レベルにはなっていないが、考え方を模索してみた。
1、2、3、4、5、6、7、8 を、2つのグループ(奇数組、偶数組)に分け、「+」「−」を
2個ずつ適切にそれらの数に付加して、それぞれのグループでの総和が 0 になるよう
にすればよい。
(例) 横軸グループ : +1−3−5+7=0
縦軸グループ : +2−4−6+8=0
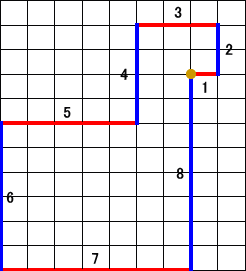
上記のパターン以外に
横軸グループ : +1−3−5+7=0 、縦軸グループ : −2+4+6−8=0
横軸グループ : −1+3+5−7=0 、縦軸グループ : +2−4−6+8=0
横軸グループ : −1+3+5−7=0 、縦軸グループ : −2+4+6−8=0
というパターンもあり、位数8の散歩コースは、4通りかな?
(コメント) 順列・組合せの計算で求められるような...予感!
上記の解について、横軸方向に関して対称なもの、縦軸方向に関して対称なものを同一
視すれば、
横軸グループ : +1−3−5+7=0
縦軸グループ : +2−4−6+8=0
の1通りが求めるものとなる。(平成22年1月4日付け GAI さんの結果を参考にした)
(実際の散策コースとしては、4通り×2=8通り?)
次に、位数16の散歩コースとしては、次の横軸グループからの1つと縦軸グループから
の1つを組み合わせればいいだろう。
横軸グループ
(X1) +1+3−5−7−9−11+13+15=0
(X2) +1−3+5−7−9+11−13+15=0
(X3) +1−3−5+7+9−11−13+15=0
(X4) +1−3−5+7−9+11+13−15=0
(X5) −1+3+5−7+9−11−13+15=0
(X6) −1+3+5−7−9+11+13−15=0
(X7) −1+3−5+7+9−11+13−15=0
(X8) −1−3+5+7+9+11−13−15=0
縦軸グループ
(Y1) +2+4+6+8−10−12−14+16=0
(Y2) +2+4+6−8+10−12+14−16=0
(Y3) +2+4−6+8+10+12−14−16=0
(Y4) +2+4−6−8−10−12+14+16=0
(Y5) +2−4+6−8−10+12−14+16=0
(Y6) +2−4−6+8+10−12−14+16=0
(Y7) +2−4−6+8−10+12+14−16=0
(Y8) −2+4+6−8+10−12−14+16=0
(Y9) −2+4+6−8−10+12+14−16=0
(Y10) −2+4−6+8+10−12+14−16=0
(Y11) −2−4+6+8+10+12−14−16=0
(Y12) −2−4+6−8−10−12+14+16=0
(Y13) −2−4−6+8−10+12−14+16=0
(Y14) −2−4−6−8+10+12+14−16=0
問題は、これらを組み合わせて、コースが交錯しないかどうかである。
例えば、(X1)(Y1)は、
横軸グループ : +1+3−5−7−9−11+13+15=0
横軸グループ : +2+4+6+8−10−12−14+16=0
なので、

となり、求める解である。
しかるに、(X7)(Y5)は、
横軸グループ : −1+3−5+7+9−11+13−15=0
横軸グループ : +2−4+6−8−10+12−14+16=0
なので、
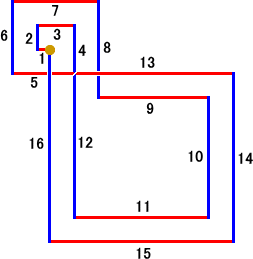
となり、途中で線が交錯して、求める解にはならない。
一体、この差はどこから来るのだろうか?
以下、8×14=112の全パターンについて、一つ一つチェックしてみよう。
(X1)(Y1)、(X1)(Y4)、(X1)(Y7)、(X1)(Y8)、(X1)(Y11)、(X1)(Y14)は、解である。
(X1)(Y2)、(X1)(Y3)、(X1)(Y5)、(X1)(Y6)、(X1)(Y9)、(X1)(Y10)、(X1)(Y12)、
(X1)(Y13)は、解でない。
また、(Xm)(Yn) (m=2、3、4 n=1、2、・・・、13、14) も、解でない。
ところで、 (X5)=−(X4) 、(X6)=−(X3) 、(X7)=−(X2) 、(X8)=−(X1)
(Y8)=−(Y7) 、(Y9)=−(Y6) 、(Y10)=−(Y5) 、(Y11)=−(Y4) 、
(Y12)=−(Y3) 、(Y13)=−(Y2) 、(Y14)=−(Y1)
であることに注意すると、
(X5)(Y1)={−(X4)}{−(Y14)} より、(X5)(Y1)は、(X4)(Y14)とスタート地点に関
して点対称となるので、解にはならない。
同様にして、
(Xm)(Yn) (m=5、6、7 n=1、2、・・・、13、14) も、解にはならない。
(X8)(Y1)は(X1)(Y14)と、(X8)(Y4)は(X1)(Y11)と、(X8)(Y7)は(X1)(Y8)と、
(X8)(Y8)は(X1)(Y7)と、(X8)(Y11)は(X1)(Y4)と、(X8)(Y14)は(X1)(Y1)と、
それぞれスタート地点に関して点対称となるので、解になる。
それに対して、
(X8)(Y2)、(X8)(Y3)、(X8)(Y5)、(X8)(Y6)、(X8)(Y9)、(X8)(Y10)、
(X8)(Y12)、(X8)(Y13)は、解にはならない。
以上から、位数16の散歩コースは、次の12通りである。
(X1)(Y1)、(X1)(Y4)、(X1)(Y7)、(X1)(Y8)、(X1)(Y11)、(X1)(Y14)、
(X8)(Y1)、(X8)(Y4)、(X8)(Y7)、(X8)(Y8)、(X8)(Y11)、(X8)(Y14)
上記の解について、横軸方向に関して対称なもの、縦軸方向に関して対称なものを同一
視すれば、
(X1)(Y1) 、(X1)(Y4) 、(X1)(Y7)
の3通りが求めるものとなる。(平成22年1月4日付け GAI さんの結果を参考にした)
(コメント) 実際の散歩コースとしては、12通り×2=24通りあるのかな?
次に、位数24の散歩コースの考察に移ろう。
位数16の散歩コースのときと同様に、次の横軸グループからの1つと縦軸グループから
の1つを組み合わせればよい。ただし、その中には、解になるものと解にならないものが共
存している。
横軸グループ
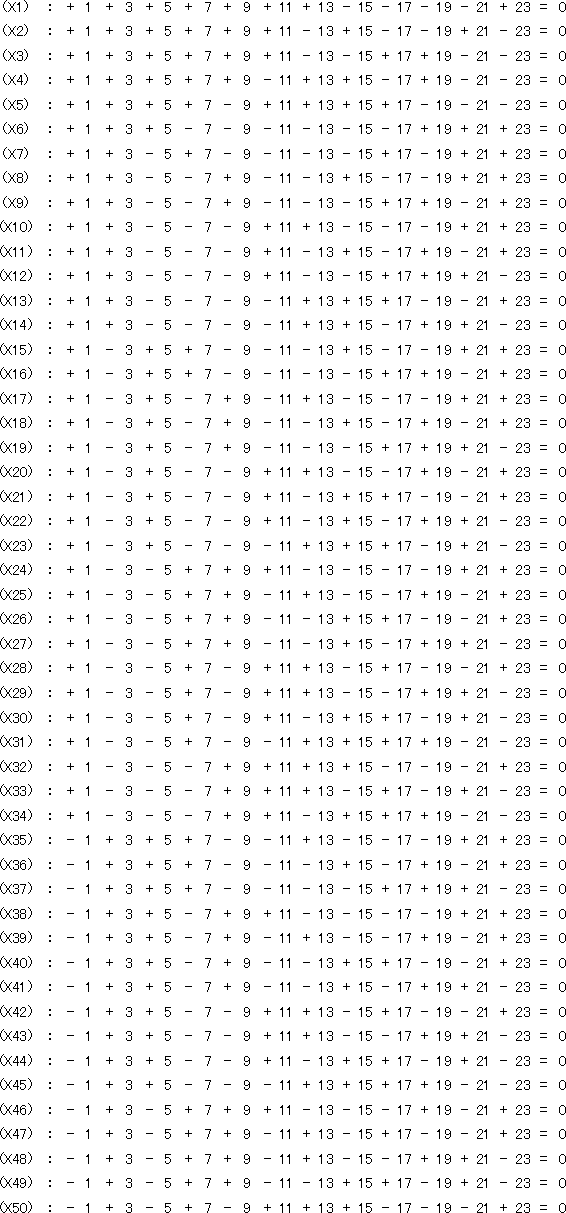

縦軸グループ
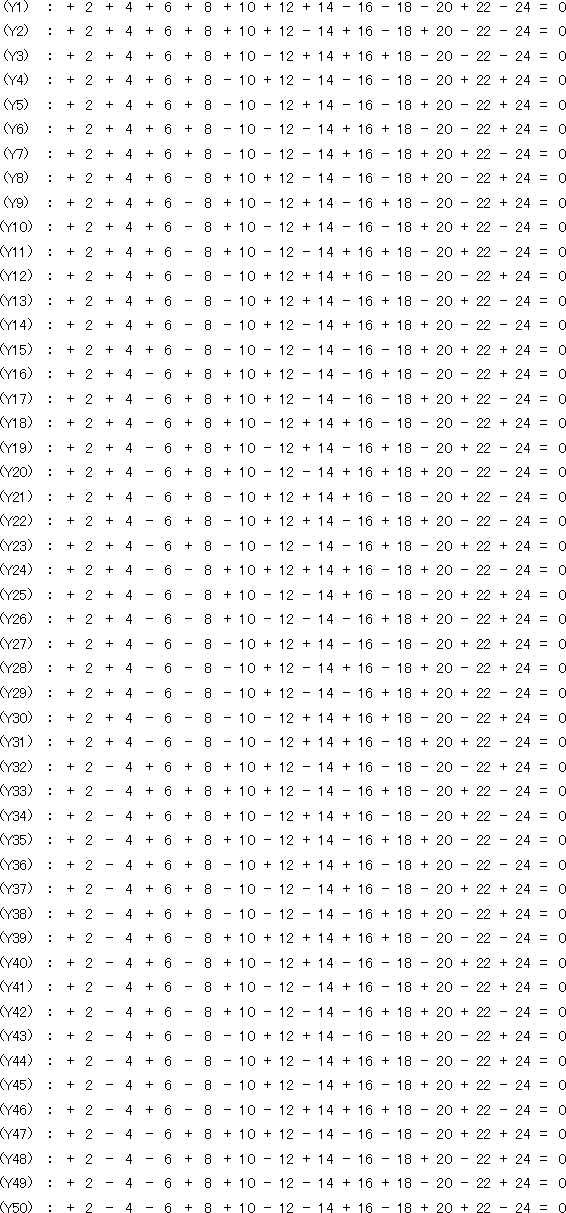
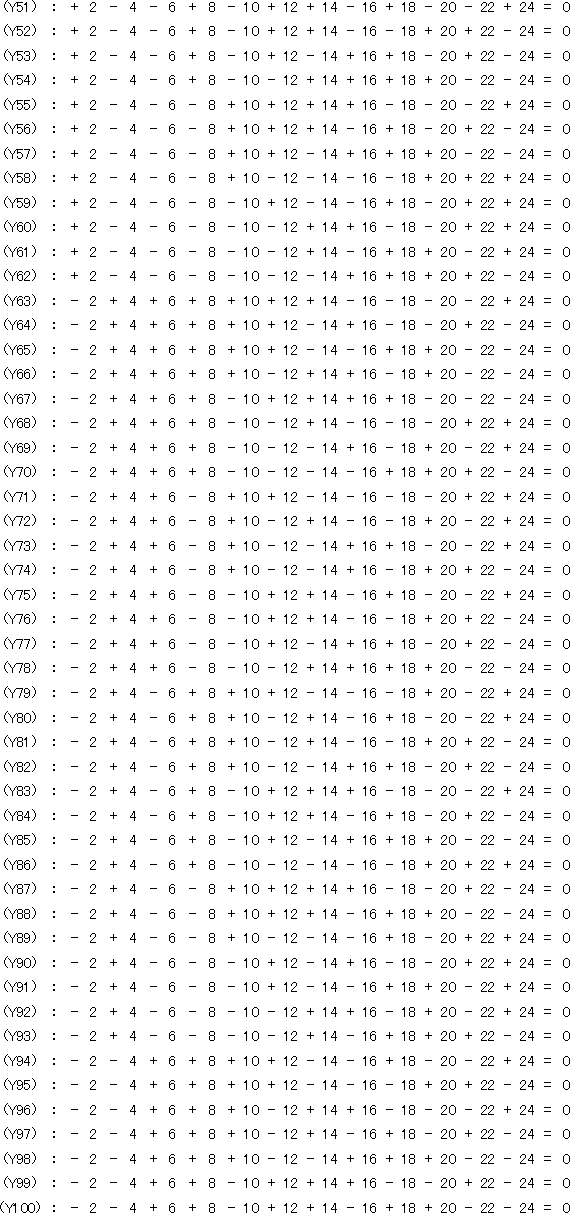

(コメント) これから手計算で解を探索するのですが、数が多すぎ...ですね。
平成22年1月4日付けで、GAI さんより、位数24の散策コースの解をいただいた。
横軸方向に関して対称なもの、縦軸方向に関して対称なものを同一視して、67通りある
とのことである。(ということは、実際の散策コースとしては、268通り×2=536通り?)
プログラムを作って総当りの組み合わせで調べつくせば何とかなるのではないかと感じた
とのことで、コンピュータに詳しい方にプログラムを作成してもらい、正月の3日間働かし続
けられたそうです。(コンピューターはお雑煮もおせちも食べずに頑張ったとか...。)
思ったよりも多様なコースが構成できることが驚きで、そのコースが図形的に面白かった
とのこと。
本来だと、GAIさんの求められた解を図形として紹介すべきところですが、紙面に限りがあ
るので簡略化して紹介したいと思う。
(詳しい図は、当HPの掲示板「出会いの泉」にてご覧下さい。)
掲示板投稿NUM: 1、2、3、4、5、6、7、8、9、10、11、12、13、
14、15、16、17、18、19、20、21、22、23
(X1)(Y3)、(X1)(Y4)、、(X1)(Y7)、(X1)(Y12)、(X1)(Y15)、(X1)(Y17)、
(X1)(Y18)、(X1)(Y23)、(X1)(Y24)、(X1)(Y29)、(X1)(Y30)、(X1)(Y36)、
(X1)(Y37)、(X1)(Y39)、(X1)(Y42)、(X1)(Y47)、(X1)(Y54)、(X1)(Y55)、
(X1)(Y58)、(X1)(Y59)、(X1)(Y62)、(X4)(Y47)、(X4)(Y54)、(X4)(Y57)、
(X5)(Y12)、(X5)(Y14)、(X5)(Y15)、(X5)(Y18)、(X5)(Y20)、(X5)(Y27)、
(X5)(Y29)、(X5)(Y32)、(X5)(Y35)、(X5)(Y46)、(X5)(Y47)、(X5)(Y62)、
(X6)(Y4)、(X6)(Y8)、(X6)(Y12)、(X6)(Y15)、(X6)(Y29)、(X6)(Y32)、
(X6)(Y37)、(X6)(Y57)、(X6)(Y62)、(X7)(Y4)、(X8)(Y18)、(X12)(Y23)、
(X7)(Y57)、(X7)(Y62)、(X10)(Y62)、(X12)(Y15)、(X12)(Y39)、(X12)(Y54)、
(X12)(Y57)、(X14)(Y15)、(X14)(Y39)、(X15)(Y4)、(X15)(Y16)、(X15)(Y18)、
(X22)(Y15)、(X24)(Y12)、(X24)(Y15)、(X24)(Y32)、(X31)(Y32)、(X32)(Y4)、
(X32)(Y47) 以上 67パターン
(コメント) 年越しのパズルが解決してスッキリしました。GAI さんに感謝します。
また、当HPがいつもお世話になっているHN「らすかる」さんが、プログラムを作って調べ
られた結果、以下のとおりになったとのことである。
位数 8 : 1通り
位数 16 : 3通り
位数 24 : 67通り
位数 32 : 1259通り (実行時間:0.3秒)
位数 40 : 41381通り (実行時間:9秒)
位数 48 :1651922通り (実行時間:12分半)
(コメント) 鮮やかです!らすかるさんに感謝します。