
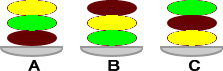
3つのお皿 A、B、C に茶、黄緑、黄の3色の団子が3個ずつ、下図のように積まれている。

3つのお皿間で団子を移し変えて、下図のようにしたい。どのように移したらよいか。但し、団
子を移すときは、移したい団子の上の団子も上下関係を変えないで一緒に移すものとする。
(答) 次のように移せばよい。

(追記) 当HPがいつもお世話になっているFNさんが、この問題について考察されました。
(平成22年6月10日付け)
上記の問題で、茶、黄緑、黄の色を順に数字の1、2、3に置き換え、上に積むことを横に
並べると考えることにする。すると、問題は次のように言い換えられる。
9個の数字の並び (111,222,333) を、次の操作を何回か行って、 (123,231,312) と
いう並びにしたい。
(操作) 3つの成分(111等を成分と呼ぶことにする)のうちの1つの右から何個か取って、
順序を変えずに他の成分の右に付け加える。
このとき、できるだけ短い手数でするにはどのようにすればよいか。
解答では、6手でできることが書いてあるが、6手が最短であることは次のようにして示さ
れる。(FNさんより平成22年6月13日付け・・・一部多少文言等を修正させていただきました!)
(証明) 1→2→3→1 を正順とし、正順となる対の個数を正順数と呼ぶことにする。
たとえば、(111,222,333) の正順数は0である。
(123,231,312) の正順数は6である。(12と23、23と31、31と12)
ところで、「3つの成分のうちの1つの右から何個か取って、順序を変えずに他の
成分の右に付け加える」という操作で、正順数がどう変わるかを考える。
1回の操作で、
1つの成分の右から何個かを取るとき、正順数の変化は、0 または −1
それを他の成分の右に付け加えるとき、正順数の変化は、0 または +1
である。 すなわち、1回の操作で正順数は高々1しか増えない。
したがって、正順数0の状態から正順数6の状態にするには、少なくとも6回の操
作が必要である。実際に6手で可能なので、6手が最短である。 (証終)
(コメント) このようなタイプの証明法に初めて触れました。正順数に注目するというテクニ
ックに感動しました!FNさんに感謝します。
さらに、FNさんから問題が提起された。
お皿が4つで団子が4個の場合、すなわち (1111,2222,3333,4444) に対して、上の
操作をできるだけ少ない回数行って、(1234,2341,3412,4123) にしてください。
このFNさんの問いかけに対して、当HPがいつもお世話になっているGAI さんが解答を示
された。(平成22年6月12日付け)
(1111 ,2222 ,3333 ,4444 )
→ (111 ,2222 ,3333 ,44441 )
→ (1112 ,222 ,3333 ,44441 )
→ (1112 ,22 ,3333 ,444412 )
→ (11123 ,22 ,333 ,444412 )
→ (11123 ,223 ,33 ,444412 )
→ (11123 ,2234412 ,33 ,44 )
→ (1 ,2234412 ,33 ,441123 )
→ (1234412 ,2 ,33 ,441123 )
→ (1234412 ,23 ,3 ,441123 )
→ (1234 ,23 ,3412 ,441123 )
→ (1234 ,2341123 ,3412 ,4 )
→ (1234 ,2341 ,3412 ,4123 )
以上、12手で可能。これは、最短?
FNさんによれば、12手が最短手数で、3皿3個の6手が最短であることと、4皿4個の12
手が最短であることは同様に証明できるとのこと。(平成22年6月12日付け)
同様にして、n 皿 n 個の場合、少なくとも n(n−1)手はかかるが、これが最短手数であ
る可能性がありそうだとのことである。
このことに関連して、GAI さんは、5 皿 5 個の場合に、20手でできることを見出された。
FNさんの示唆することを考えれば、最短手数となる。(平成22年6月14日付け)
(11111,22222,33333,44444,55555)
→ (1,22222,33333,44444,555551111)
→ (1,22,33333,44444,555551111222)
→ (12,2,33333,44444,555551111222)
→ (12,2,333,44444,55555111122233)
→ (123,2,33,44444,55555111122233)
→ (1234,2,33,4444,55555111122233)
→ (1234,2,33,444,555551111222334)
→ (1234,23,3,444,555551111222334)
→ (1234,234,3,44,555551111222334)
→ (1234,234,34,4,555551111222334)
→ (123455551111222334,234,34,4,5)
→ (12345,2345551111222334,34,4,5)
→ (12345,2345,34551111222334,4,5)
→ (12345,2345,345,451111222334,5)
→ (12345,2345111222334,345,451,5)
→ (12345,23451,34511222334,451,5)
→ (12345,23451,3451,451,51222334)
→ (12345,23451,345122334,451,512)
→ (12345,23451,34512,4512334,512)
→ (12345,23451,34512,45123,51234)
以上 20手
(コメント) 上記手順は、GAI さんが示されたものと一部異なる。手数は20手でもいろいろ
な手順があるということが分かった。でも、これは当然かな?
手順を発見されたGAI さんに感謝します。
さらに、GAI さんは、6 皿 6 個の場合に、30手でできることを見出された。
(平成22年6月16日付け)
(111111,222222,333333,444444,555555,666666)
→(1,222222,333333,444444,555555,66666611111)
→(1,22,333333,444444,555555,666666111112222)
→(12,2,333333,444444,555555,666666111112222)
→(12,2,333,444444,555555,666666111112222333)
→(123,2,33,444444,555555,666666111112222333)
→(123,23,3,444444,555555,666666111112222333)
→(123,23,3,4444,555555,66666611111222233344)
→(123,23,3,4444,55555,666666111112222333445)
→(1234,23,3,444,55555,666666111112222333445)
→(1234,234,3,44,55555,666666111112222333445)
→(1234,234,34,4,55555,666666111112222333445)
→(12345,234,34,4,5555,666666111112222333445)
→(12345,2345,34,4,555,666666111112222333445)
→(12345,2345,345,4,55,666666111112222333445)
→(12345,2345,345,45,5,666666111112222333445)
→(1234566666111112222333445,2345,345,45,5,6)
→(123456,23456666111112222333445,345,45,5,6)
→(123456,23456,345666111112222333445,45,5,6)
→(123456,23456,3456,4566111112222333445,5,6)
→(123456,23456,3456,456,56111112222333445,6)
→(123456,23456,3456,456,561,611112222333445)
→(123456,234561112222333445,3456,456,561,61)
→(123456,234561,3456112222333445,456,561,61)
→(123456,234561,34561,45612222333445,561,61)
→(123456,234561,34561,45612,561222333445,61)
→(123456,234561,3456122333445,45612,5612,61)
→(123456,234561,345612,45612,5612,612333445)
→(123456,234561,345612,4561233445,5612,6123)
→(123456,234561,345612,456123,56123445,6123)
→(123456,234561,345612,456123,561234,612345)
以上 30手
GAI さんによれば、最後のところで少し考慮する部分がでてくるが、ここをクリアーすれば
他はほぼ機械的に出来るとのことです。
FNさんから、「6の列に1を5個、2を4個、3を3個と1個ずつ減らしながら積んでいくという
15手目の形を作るのがキーポイントだったようですね。」とコメントが寄せられました。
(平成22年6月16日付け)