
次のように8個の数字を4枚ずつ2つの組A、Bに分ける。
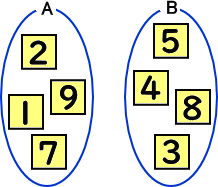
Aに含まれる数字の合計は19。Bに含まれる数字の合計は20。
今、A、Bそれぞれのカードから1枚ずつ交換して、合計が同じになるようにしたい。
どうすればいいのだろうか?
(答) 例えば、9と8を交換し、9を180度回転させて、6として考えればよい。合計は18。
#こういう答えは有りか?
よおすけさんからのコメントです。(令和2年2月5日付け)
2と5を交換→Aの和:22、Bの和:17となり不適
2と4を交換→Aの和:21、Bの和:18となり不適
2と8を交換→Aの和:25、Bの和:14となり不適
2と3を交換→Aの和:20、Bの和:19となり不適
9と5を交換→Aの和:15、Bの和:24となり不適
9と4を交換→Aの和:14、Bの和:25となり不適
9と8を交換→Aの和:18、Bの和:21となり不適
9と3を交換→Aの和:13、Bの和:26となり不適
1と5を交換→Aの和:23、Bの和:16となり不適
1と4を交換→Aの和:22、Bの和:17となり不適
1と8を交換→Aの和:26、Bの和:13となり不適
1と3を交換→Aの和:21、Bの和:18となり不適
7と5を交換→Aの和:17、Bの和:22となり不適
7と4を交換→Aの和:16、Bの和:23となり不適
7と8を交換→Aの和:20、Bの和:19となり不適
7と3を交換→Aの和:15、Bの和:24となり不適
「9を180度回転させて、6として考える」を使わないパターンは上記の通りだが、いずれも
A、Bそれぞれの合計が同じになるものはないので、上記の解以外に解がなければ、それが
唯一解であると思われる。
DD++さんからのコメントです。(令和2年2月5日付け)
全パターン頑張らなくても、「合計が一致するなら8枚の合計は偶数のはず」で終わります
ね。
らすかるさんからのコメントです。(令和2年2月5日付け)
「上記の解以外に解がなければ、それが唯一解」は当然ですが、他に、
「9を180°回転し、1と3を交換する」 と 「9を180°回転し、2と4を交換する」
という答えがあり、全部で、3通りだと思います。
(コメント) 3通りも解があるんですね!想定外でした。らすかるさんに感謝します。