石取りゲーム（２）　　　　　　　　　　　　　　　　　　　　　　　　　　戻る

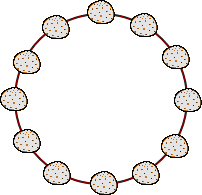
　　　左図のように、円周上に、１２個の石が置いてある。

　　　二人のプレーヤーが、交互に、１個または連続する
　　２個の石を取り合って、最後に残った石を取った人が
　　勝ちというゲームを行う。

　　このゲームは先手・後手どちらが有利であろうか？

　　ただし、石が取られた後の円周上に並んでいる状態
　　から、隣り合っている石は、「連続」と判断するものと
　　する。


































（答）　 後手必勝である。先手がどういうとり方をしても、必ず残りの個数が、３の倍数にな
　　　　るようなとり方をして先手に手を渡せばよい。

　　　　（参考文献　：　ピーター・フランクル　著　問題集（２）　（日本評論社））