三段跳び　　　　　　　　　　　　　　　　　　　　　　　

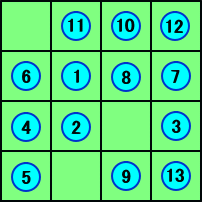
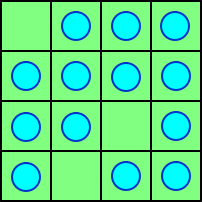
今、左図のような４×４の碁盤上に、１３個の碁石が置 　　いてある。これらの碁石のどこかから始めて、次のルー 　　ルに従って、碁石を盤上から取り去っていくというパズル 　　を考える。 　　（ルール）　１．　まず、最初の碁石（Ａ）を取り去る。 　　　　　　　　　２．　次に、その碁石（Ａ）から１マス、上下左 　　　　　　　　　　　右に跳んで、碁石（Ｂ）を取り去る。 　　　　　　　　　３．　次に、その碁石（Ｂ）から２マス、上下左 　　　　　　　　　　　右に跳んで、碁石（Ｃ）を取り去る。 　　　　　　　　　４．　次に、その碁石（Ｃ）から３マス、上下左 　　　　　　　　　　　右に跳んで、碁石（Ｄ）を取り去る。 　　　　　　　　　５．　次に、その碁石（Ｄ）を碁石（Ａ）として、 　　　　　　　　　　　２〜４の手順を繰り返す。

　パズルの趣旨を簡単に言い表せば、１マス跳び、２マス跳び、３マス跳びを順に繰り返して、
同じ碁石を２度と通ることなく、全ての碁石が通過できるか、ということである。

　このパズルの攻略のポイントは、２マス跳びと３マス跳びの組合わせを探すことである。

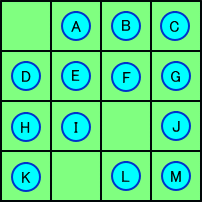左図において、そのような組合せは次の１４通りしかない。 　　　　A-C-M　　C-J-H 　　D-K-M　　E-G-D　　F-L-B 　　　　F-D-G 　 G-M-C　　G-M-K　　I-J-H　　J-C-M 　　　　K-D-G　　K-L-B 　　L-K-M 　 M-G-D 　　上記１４通りのうち、赤字の１０通りは、後が上手く続か 　ないなどの不具合がある。 　　　さらに、残った黒字の４通りについて、アルファベット 　が重複していない組合せを３つ選択すれば、 　　　　　　　Ｆ−Ｌ−Ｂ　　Ｉ−Ｊ−Ｈ　　Ｋ−Ｄ−Ｇ 　が、最適道順の候補となる。

　これらを、色分けして示せば、左下図のようになる。

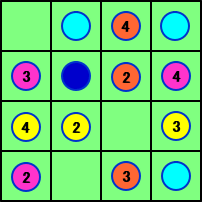２−３−４−２−３−４−２−３−４−・・・　ということを 　　考えると、自然と、上記の３つの組合せがつながってくる。 　　　従って、最初に取り去る碁石は、青色の碁石（Ｅ）と確定 　　し、最後の道順の組合せは、 　　　　　　　Ａ−Ｃ−Ｍ 　　となる。

　従って、正解の道順を番号で示せば、下図の通りとなる。