お父さんを助けろ　　　　　　　　　　　　　　　　　　　

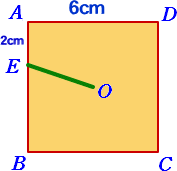
ＡＤ＝６ｃｍの正方形の形をしたケーキがある。このケー 　　キを３等分するところ、お父さんが何を思ったのか、ＯＥと 　　包丁を入れてしまった。（Ｏは正方形の中心） 　　　実はお父さんには深遠なる策略があったのだが、それ 　　に気づいてくれない家族は、「お父さんのミス！」とお父さ 　　んを責めるばかり。 　　　怒ったお父さんは、包丁を放り出して、何処かへ行って 　　しまった。

　果たして、お父さんはケーキをどう切ろうとしたのでしょうか？お父さんの意を汲んで、ケ
ーキの切り方を考えてください。




























（答）　下の線に沿って切る。

　　　多分、お父さんは、　６×６÷３＝１２　と考えて、

　　　　　（６＋ＡＥ）×３÷２＝１２　から、　ＡＥ＝２　としたのだろう。



　　　　　　　　　らすかるさんは、次のように考えられたそうです。（平成２３年５月４日付け）

　　　　　　　　　　中心Ｏから引いた直線で切り分けるとき、 (面積比)＝(周囲の長さの比)
　　　　　　　　　なので、　６×４÷３＝８　より、８−６＝２（ｃｍ）　のところから包丁を入れ
　　　　　　　　　ればよい。

　　　　　　　　　（コメント）　らすかるさんの考え方の方が簡明ですね！

　真意が伝わらなくて、かわいそうなお父さんですね！でも、日本のどこの家庭でもこんなこ
とは日常茶飯事に起こっていることかも．．．。

　そもそもケーキがキッチリ６ｃｍ×６ｃｍの正方形であることはあまり現実味がない。まして、
そのケーキを３等分するために定規でキッチリ２ｃｍを測るなんてことは普通しない。

　一般家庭では、アバウトに目分量で切り分けていると思う。ただ、兄弟が多い場合は、「そ
っちの方が多い！」「こっちは少ない！」などという感情的なバトルが起こることも．．．。

　いかに公平にケーキを切り分けるかのキーポイントは、

　　ケーキを切る人とケーキを最初に取る人を別にすることである

ということを、最近、次の書籍

　　芳沢光雄　著　　「３」の発想　（新潮選書）

で知ることができた。

　こう考えると、上記のお父さんの苦労をしなくても済むわけだ！

◇ 一つのケーキを、Ａ、Ｂ の２人で公平に分けたい場合

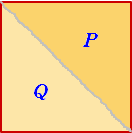　　　　まず、Ａがケーキを切る。Ａは２等分していると思っているから、

　　　Ｐ、Ｑのどちらを取ることになっても異論はない。

　　　　ＡがＰ、Ｑの２つに切り分けたケーキのうちのどちらかを、Ｂが

　　　取る。もちろん、Ｂから異論は出ない。残りをＡが取る。


　かくして、Ａ、Ｂの両者に不平不満が出ない形で、公平に２等分されたと考えてよい。

◇ 一つのケーキを、Ａ、Ｂ、Ｃ の３人で公平に分けたい場合

　この場合は、２人のときとは若干異なる手順が必要である。

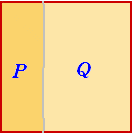　　　　まず、Ａがケーキを切る。Ａは３等分していると思っているから、

　　　Ｐを取ることになっても異論はない。

　　　　問題は、Ｂ、Ｃの意見である。２人がともにＰが１/３以下と思って

　　　くれれば、ＡはＰを取り、Ｑについての２等分の問題に帰着される。


　まず、Ｂだけが「Ｐは１/３より多いんじゃない？」と主張した場合（Ｃだけのときも同様）

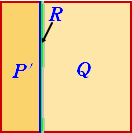　　　　Ｂに１/３になるようにＰを切らせる。すると、Ｂにとっては、Ｐ’は

　　　１/３と思っているから、Ｐ’を取ることになっても異論はない。Ｒは

　　　余りである。そこで、ＢはＰ’を取り、Ｑ＋Ｒについての２等分の問

　　　題に帰着される。


　次に、ＢおよびＣが「Ｐは１/３より多いんじゃない？」と主張した場合

　　　　Ｂに１/３になるようにＰを切らせる。すると、Ｂにとっては、Ｐ’は

　　　１/３と思っているから、Ｐ’を取ることになっても異論はない。Ｒは

　　　余りである。次に、ＣがＰ’を１/３以下と思ってくれれば、ＢはＰ’

　　　を取り、Ｑ＋Ｒについての２等分の問題に帰着される。


　問題は、Ｃが「Ｐ’はまだ１/３より多いんじゃない？」と主張する場合である。

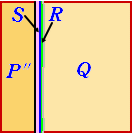
　そのときは、Ｃに１/３になるようにＰ’を切らせる。すると、Ｃにとっては、Ｐ”は１/３と思って

いるから、Ｐ”を取ることになっても異論はない。Ｓは余りである。

そこで、ＣはＰ”を取り、Ｑ＋Ｒ＋Ｓについての２等分の問題に帰着される。

（コメント）　異を唱えるものに気が済むまで切り取らせるというのが極意なんですね！最初
　　　　　　の方で切り取った人は、１/３で切り分けたと思っていて、それに余りが加わってく
　　　　　　るので、ほくそ笑むことはあっても異論が出ることはないということですか。