平方数を作る　 　　　　　　　　　　　　　　　　　　　

　１から１５までの１５個の整数を、次の条件を満たすように並べかえて下さい。

　　条件 ： 隣り合う２数の和は、常に平方数

どのように並べたらいいのでしょうか？































（答）　平方数の可能性は、　４ 、９ 、１６ 、２５　の４通りしかない。
　　　ところで、各数について、平方数となる組合せを調べると下表のようになる。

　１つの並べ方を例示すれば、次のようになる。

　　　９ 、７ 、２ 、１４ 、１１ 、５ 、４ 、１２ 、１３ 、３ 、６ 、１０ 、１５ 、１ 、８

　　　（ ６ のところで、１を選ぶ可能性もあるわけだが、この場合は不適である。）

（注）　このような性質をもつ数列は、１４以下では絶対に作れないことが知られている。

　「隣り合う２数の和が平方数」という条件から、「 １ から ｎ （ｎ≧２）までの整数」について
考えるのが自然であろう。

　いま、１ から ｎ （ｎ≧２）までの整数について、隣り合う２数の和は、常に平方数であるよ
うに並べられるものとする。そのように並べられた数列を、 Ａ ＝ ｛ ａ_ｎ ｝ とおく。

　ｎ≧２ より、　２∈Ａ　なので、　２に隣り合う数で平方数になるものが存在するためには、
７∈Ａ　でなければならない。

　よって、　｛ １、２、３、４、５、６、７ ｝⊂Ａ　である。

　このとき、　４＋５＝９　（平方数）で、４ または ５ に対して、９ 以外の平方数が存在する
必要があるので、　少なくとも １１∈Ａ　でなければならない。　すなわち、　ｎ≧１１

　よって、　｛ １、２、３、４、５、６、７、８、９、１０、１１ ｝⊂Ａ　である。

　ここで、　ｎ≦１４　と仮定する。

（参考文献：数学オリンピック財団　編　数学オリンピック１９９８〜２００３　（日本評論社））


（追記）　平成２２年１０月２６日付け

　当ＨＰがいつもお世話になっているＨＮ「ＦＮ」さんが、上記の問題の拡張を考えられた。

　ｎ を自然数とする。１から ｎ までの ｎ 個の自然数を隣り合う２数の和が常に平方
数になるように並べかえることが可能であるのは、ｎ がどのような数であるときか。

　ｎ が１４以下のとき不可能であることは証明されている。（もっとも、ｎ＝１ のときは、隣り
合う２数はないから可能とみなすこともできるが．．．。）

　上記で、ｎ＝１５　のとき可能であることは示されている。そのときの両端が９と８なので、
１６、１７をその隣におけば、その隣り合う２数は平方数になるので、ｎ＝１６、１７のときも
可能である。 ｎ＝１８、１９、２０　あたりは不可能なようである。

　ｎ＝１５、１６、１７　以外にこのような並べかえが可能な ｎ はあるのだろうか？あるとす
れば、それはどのような数であろうか？

　この問いかけについて、ＦＮさんが考察された。（平成２２年１１月　３日付け）

　ｎ≧１８　で考えるが、まず、１８≦ｎ≦２４　とする。

ｎ＝１８　のとき

　１８の隣にくるのは、７しかない。従って、１８は端で、その隣は７である。このとき、
左端が１８で、その隣が７としてよい。　１８、７、・・・

　１６の隣にくるのは、９と２０しかない。(ｎ＝１８、１９のときは、９のみ)
　２０の隣にくるのは、５と１６しかない。
　９の隣にくるのは、７と１６しかない。
　７の隣にくるのは、１８以外では、２と９しかない。

　９が右端にくるか、そうでなければ、７、９、１６　と続くしかないから、次のどちらかである。

　　（１）　１８、７、２、・・・、５、２０、１６、９
　　（２）　１８、７、９、１６、２０、５、・・・

　何れにしても、「２０」はないから、ｎ＝１８のときは不可能。

（コメント）　ｎ＝１８のとき、不可能であることは、下図のグラフを見れば一目瞭然である。
　　　　　　端点が３個存在するので、一筆書きで各数字を結ぶことはできない。

　　　　　　　　　

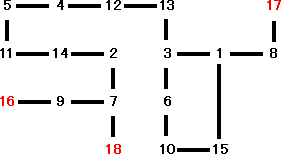
ｎ＝１９　のとき

　１９の隣にくるのは、６と１７の２つあり、１９は並びの途中に出現する。従って、ｎ＝１８の場
合と同様で、次のどちらかである。

　　（１）　１８、７、２、・・・、５、２０、１６、９
　　（２）　１８、７、９、１６、２０、５、・・・

　何れにしても、「２０」はないから、ｎ＝１９　のときは不可能。

ｎ＝２０　のとき

　５の隣は、２０以外では、４、１１だけである。
　１１の隣は、５以外では、１４だけであるから、１１は５につづけるか右端しかないから、次
のどれかである。

　　（１）　１８、７、２、・・・、１４、１１、５、２０、１６、９
　　（２）　１８、７、９、１６、２０、５、１１、１４、・・・
　　（３）　１８、７、９、１６、２０、５、４、・・・、１４、１１

　２の隣は既に使われている７、１４以外では、２３だけである。

　よって、ｎ＝２０　のときは、「２３」はないから、（１）（２）（３）の何れも不可能である。

　同様にして、ｎ＝２１、２２　のときも不可能である。

　以上で、ｎ＝１８、１９、２０、２１、２２　では不可能であることがわかったが、ｎ＝２３　のと
きは可能である。例えば、

　　１８、７、２、２３、１３、１２、４、２１、１５、１０、６、１９、１７、８、１、３、２２、１４、１１、５、２０、１６、９
　　（他にも解はあります！）

　ｎ＝２４　は不可能なようです。しかしもう少し書き方を工夫しないと大変長くなってしまい
そうです。ｎ≧２５は、ほとんど考えていません。ｎ が大きくなるほうが楽になるような気は
しますから、可能である場合が多そうですが、わかりません。

（コメント）　ＦＮさんに感謝します。

　ｎ＝３０　までの平方数になる数の組合せの表を作ってみた。

　果たして、ｎ≦３０の範囲に可能な場合はあるのだろうか？


　これに対して、らすかるさんが調査されました。（平成２２年１１月４日付け）

　ｎ＝４０　ぐらいまで計算して、数列サイトで検索しました。

　　　http://www.research.att.com/~njas/sequences/A071983

　ｎ＝１５〜４５の解が何通りあるかが書かれています。解の一例を以下に書きます。３２以
上では巡回解（先頭と末尾の和も平方数）がありますので、巡回解の一例を書いています。

15：8 1 15 10 6 3 13 12 4 5 11 14 2 7 9

16：8 1 15 10 6 3 13 12 4 5 11 14 2 7 9 16

17：16 9 7 2 14 11 5 4 12 13 3 6 10 15 1 8 17

23：9 16 20 5 11 14 22 3 1 8 17 19 6 10 15 21 4 12 13 23 2 7 18

25：9 16 20 5 4 21 15 10 6 19 17 8 1 3 22 14 11 25 24 12 13 23 2 7 18

26：9 16 20 5 11 25 24 12 4 21 15 1 8 17 19 6 10 26 23 13 3 22 14 2 7 18

27：18 7 2 14 11 5 20 16 9 27 22 3 13 23 26 10 6 19 17 8 1 15 21 4 12 24 25

28：18 7 2 14 11 5 20 16 9 27 22 3 6 19 17 8 28 21 4 12 13 23 26 10 15 1 24 25

29：18 7 29 20 16 9 27 22 3 13 12 4 5 11 14 2 23 26 10 6 19 17 8 28 21 15 1 24 25

30：18 7 29 20 16 9 27 22 3 13 12 4 5 11 14 2 23 26 10 6 30 19 17 8 28 21 15 1 24 25

31：1 15 10 6 30 19 17 8 28 21 4 5 31 18 7 29 20 16 9 27 22 3 13 12 24 25 11 14 2 23 26

32：1 8 28 21 4 32 17 19 30 6 3 13 12 24 25 11
　　　　　5 31 18 7 29 20 16 9 27 22 14 2 23 26 10 15

33：1 8 28 21 4 32 17 19 30 6 3 13 12 24 25 11
　　　　　5 20 29 7 18 31 33 16 9 27 22 14 2 23 26 10 15

34：1 3 13 12 4 32 17 8 28 21 15 34 30 19 6 10
　　　　 26 23 2 14 22 27 9 16 33 31 18 7 29 20 5 11 25 24

35：1 3 6 19 30 34 2 7 18 31 33 16 9 27 22 14 11
　　　　 25 24 12 13 23 26 10 15 21 28 8 17 32 4 5 20 29 35

36：1 3 6 19 30 34 2 23 26 10 15 21 4 32 17 8 28
　　　　 36 13 12 24 25 11 5 20 29 7 18 31 33 16 9 27 22 14 35

37：1 3 22 14 35 29 20 5 11 25 24 12 37 27 9 16 33
　　　　 31 18 7 2 34 15 21 4 32 17 19 30 6 10 26 23 13 36 28 8

38：1 3 33 16 9 7 18 31 5 20 29 35 14 22 27 37 12
　　　　 13 36 28 8 17 32 4 21 15 10 6 19 30 34 2 23 26 38 11 25 24

39：1 3 22 14 2 7 18 31 33 16 9 27 37 12 24 25 39
　　　　 10 6 19 30 34 15 21 4 32 17 8 28 36 13 23 26 38 11 5 20 29 35

40：1 3 6 19 30 34 2 7 18 31 33 16 9 40 24 25 39 10
　　　　 15 21 28 36 13 23 26 38 11 5 20 29 35 14 22 27 37 12 4 32 17 8

41：1 3 6 10 39 25 24 12 37 27 22 14 35 29 20 5 11 38
　　　　 26 23 13 36 28 8 41 40 9 16 33 31 18 7 2 34 30 19 17 32 4 21 15

42：1 3 6 10 15 21 4 32 17 19 30 34 2 14 22 27 37 12 24
　　　　 25 39 42 7 18 31 33 16 9 40 41 8 28 36 13 23 26 38 11 5 20 29 35

43：1 3 6 10 15 21 43 38 26 23 2 34 30 19 17 32 4 5 11 14
　　　　 22 42 39 25 24 40 41 8 28 36 13 12 37 27 9 7 18 31 33 16 20 29 35

44：1 3 6 10 15 21 43 38 26 23 2 34 30 19 17 32 4 5 11 14
　　　　 22 27 9 16 33 31 18 7 42 39 25 24 40 41 8 28 36 13 12 37 44 20 29 35

45：1 3 6 10 15 21 43 38 26 23 13 12 24 25 39 42 22 14 11 5
　　　　 44 37 27 9 40 41 8 28 36 45 4 32 17 19 30 34 2 7 18 31 33 16 20 29 35

46：1 3 6 10 15 21 43 38 26 23 13 12 24 25 39 42 22 14 11 5
　　　　 44 37 27 9 40 41 8 28 36 45 4 32 17 19 30 34 2 7 29 20 16 33 31 18 46 35

47：1 3 6 10 15 21 43 38 26 23 13 12 4 32 17 47 2 34 30 19 45
　　　　 36 28 8 41 40 9 7 29 20 16 33 31 18 46 35 14 11 5 44 37 27 22 42 39 25 24

48：1 3 6 10 15 21 43 38 26 23 13 12 4 32 17 47 2 34 30 19 45
　　　　 36 28 8 41 40 9 7 29 20 16 48 33 31 18 46 35 14 11 5 44 37 27 22 42 39 25 24

49：1 3 6 10 15 49 32 4 5 11 14 2 7 9 27 22 42 39 25 24 40 41 8
　　　　 17 47 34 30 19 45 36 28 21 43 38 26 23 13 12 37 44 20 29 35 46 18 31 33 16 48

50：1 3 6 10 15 49 32 4 5 11 14 50 31 18 46 35 29 7 9 27 22 42 39
　　　　 25 24 40 41 8 17 47 2 34 30 19 45 36 28 21 43 38 26 23 13 12 37 44 20 16 33 48

（コメント）　ｎ＝２５、２６、２７、２８、２９、３０、・・・　と解は存在するんですね！らすかるさん
　　　　　　に感謝します。


　上記で、ＦＮさんは、ｎ＝２３のときの一つの並び

　　１８、７、２、２３、１３、１２、４、２１、１５、１０、６、１９、１７、８、１、３、２２、１４、１１、５、２０、１６、９

をあげられ、「他にも解はあります！」とのことだった。らすかるさんのあげられた並びは、
ＦＮさんのものと同じである。

　他の解を探索するために、上記で求めた表をグラフ化してみた。（ただし、ｎ＝２３）

　　　　　

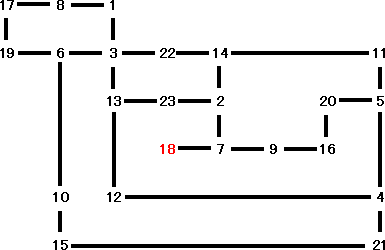
　このグラフを用いると、他の並びとして、

　　１８、７、９、１６、２０、５、１１、１４、２２、３、１、８、１７、１９、６、１０、１５、２１、４、１２、１３、２３、２

　　１８、７、９、１６、２０、５、１１、１４、２、２３、１３、１２、４、２１、１５、１０、６、１９、１７、８、１、３、２２

の２つがあることが分かる。



　　　以下工事中