
いま、1から18までの数が書かれたカードが、横一列に並んでいる。
この18枚のカードを左側から順番に下記のように3列に並べる。

上の並びにおいて、右上から下に向かって順番に、下記のように横一列に並べ替える。
このような操作を繰り返す。この操作を何回繰り返したら、下記のような場合となるか?
(答) 何はともあれ腕力で求めてみよう。
シャッフル 
いま、1から18までの数が書かれたカードが、横一列に並んでいる。
![]()
この18枚のカードを左側から順番に下記のように3列に並べる。

上の並びにおいて、右上から下に向かって順番に、下記のように横一列に並べ替える。
![]()
このような操作を繰り返す。この操作を何回繰り返したら、下記のような場合となるか?
![]()
(答) 何はともあれ腕力で求めてみよう。
| (1) | (2) | (3) | (4) | (5) | ||||||||||||||
| 1 | 2 | 3 | 3 | 6 | 9 | 9 | 18 | 8 | 8 | 16 | 5 | 5 | 10 | 15 | ||||
| 4 | 5 | 6 | 12 | 15 | 18 | 17 | 7 | 16 | 13 | 2 | 10 | 1 | 6 | 11 | ||||
| 7 | 8 | 9 | 2 | 5 | 8 | 6 | 15 | 5 | 18 | 7 | 15 | 16 | 2 | 7 | ||||
| 10 | 11 | 12 | 11 | 14 | 17 | 14 | 4 | 13 | 4 | 12 | 1 | 12 | 17 | 3 | ||||
| 13 | 14 | 15 | 1 | 4 | 7 | 3 | 12 | 2 | 9 | 17 | 6 | 8 | 13 | 18 | ||||
| 16 | 17 | 18 | 10 | 13 | 16 | 11 | 1 | 10 | 14 | 3 | 11 | 4 | 9 | 14 | ||||
| (6) | (7) | (8) | (9) | |||||||||||||||
| 15 | 11 | 7 | 7 | 14 | 2 | 2 | 4 | 6 | 6 | 12 | 18 | |||||||
| 3 | 18 | 14 | 9 | 16 | 4 | 8 | 10 | 12 | 5 | 11 | 17 | |||||||
| 10 | 6 | 2 | 11 | 18 | 6 | 14 | 16 | 18 | 4 | 10 | 16 | |||||||
| 17 | 13 | 9 | 13 | 1 | 8 | 1 | 3 | 5 | 3 | 9 | 15 | |||||||
| 5 | 1 | 16 | 15 | 3 | 10 | 7 | 9 | 11 | 2 | 8 | 14 | |||||||
| 12 | 8 | 4 | 17 | 5 | 12 | 13 | 15 | 17 | 1 | 7 | 13 | |||||||
以上から、求める操作の回数は、9回であることが分かる。
枚数が少ない場合は、上記のような腕力も通用するが、枚数が多くなると、腕力だけでは
とうてい抗しきれない。
元の配列の左側から m 番目の数が、新しい配列の左側から n 番目に移されるとき、実
は、m と n には、次のような関係式が成り立つ。
m≡3n (mod 19) (← 19 は、配列の個数(18)+1)
実際に、1≦n≦6 のとき、m=3n
7≦n≦12 のとき、m=3(n−7)+2=3n−19
13≦n≦18 のとき、m=3(n−13)+1=3n−38 から明らかである。
従って、k回目に求める配列になるためには、
3k≡−1 (mod 19)
を満たす k を求めればよい。実際に、このとき、
m≡3kn≡−n から、n≡−m≡19−m (mod 19)
が成り立つ。
ところで、33≡8、34≡3、35≡15、36≡7、37≡2、38≡6、39≡−1 (mod 19)
なので、9回目で求める配列になることが分かる。
一般に、1から 3n までの数の配列を逆順に配列し直すのに要する操作の回数
k は、
3k≡−1 (mod 3n+1)
を満たす。
ただし、このような k がいつも存在するとは限らない。
実際に、n=2 のとき、
1、2、3、4、5、6
3、6、2、5、1、4
2、4、6、1、3、5
6、5、4、3、2、1 33≡−1 (mod 7)
であるが、n=4 のとき、
1、2、3、4、5、6、7、8、9、10、11、12
3、6、9、12、2、5、8、11、1、4、7、10
9、5、1、10、6、2、11、7、3、12、8、4
1、2、3、4、5、6、7、8、9、10、11、12
33≡1 (mod 13)
となり、
3k≡−1 (mod 13)
であるような k は、決して存在しない。
以上から、逆順に配列可能かどうかは、3k≡−1 (mod 3n+1)を満たす k が存在
するかどうかによって判断することができる。
(参考文献:数学オリンピック財団編 数学オリンピック(1997〜2002) (日本評論社))
(追記) 平成20年11月24日付け
当HPがいつもお世話になっている「GAI」さんが、新しいシャッフルの方法を考えられた
という。(当HPの掲示板「出会いの泉」より転載)
「お茶の時間」を見ていたら、「シャッフル」という項目があり、カードをいくつかの山に分
け、混ぜていくやり方が記述されていた。カードマジックに利用できそうだと感じたので、
シャッフルの方法を少し変更してみた。
何枚かのカードを裏向きで手に持ち、トップから一枚ずつ裏向きのままテーブルに左か
ら右へ3枚並べる。(3山でのシャッフル)元に戻って、2枚目のカードを左から右へと重
ねる。こうして手持ちのカードが無くなるまで続ける。(手持ちのカードは3の倍数。)
次に、左の山を持ち上げ、隣の山の上に重ねて、この重ねた山を再び持ちあげて右の
山へ重ねて一つにする。これを一回のシャッフルとする。
このシャッフルを繰り返して、元の状態に復元する回数を、トランプの枚数と山の数で
調査してみたところ、次の結果を得た。カードマジックをやる上では、これ位の山が妥
当であろう。
同様に、4山でのシャッフルも考えられる。
| <3山でのシャッフル> | <4山でのシャッフル> | ||||||
| カード枚数 | 正順回数 | 逆順回数 | カード枚数 | 正順回数 | 逆順回数 | ||
| 6 | 3 | 8 | 6 | 3 | |||
| 9 | 4 | 2 | 12 | 3 | |||
| 12 | 6 | 3 | 16 | 4 | 2 | ||
| 15 | 4 | 20 | 6 | 3 | |||
| 18 | 9 | 24 | 5 | ||||
| 21 | 10 | 5 | 28 | 7 | |||
| 24 | 20 | 10 | 32 | 10 | 5 | ||
| 27 | 3 | 36 | 9 | ||||
| 30 | 15 | 40 | 5 | ||||
| 33 | 16 | 8 | 44 | 6 | |||
| 36 | 9 | 48 | 42 | 21 | |||
| 39 | 4 | 52 | 13 | ||||
| 42 | 21 | ||||||
| 45 | 22 | 11 | |||||
| 48 | 21 | ||||||
| 51 | 6 | ||||||
GAI さんによれば、これを眺めると、意外にも混ぜているように見せかけて、元に戻すこ
とが起こる現象をつくることが可能であることが分かったとのこと。27枚での3山か、20枚
での4山あたりが使えそう。
GAI さんに触発されて、Excel のVBAを利用して、「カード枚数 48」の場合のシャッフル
状況を一覧にしてみた。

(コメント) 綺麗に逆順に並んで、感動的ですね!
(追記) 平成20年11月26日付け
GAI さんから、さらに次のような情報がもたらされた。
48枚のカードなら、21回のシャッフルで逆順に戻る。
(つまり正順に並べるのに42回もかかる)
このシャッフルの方法を他の掲示板(プログラムをチェックするサイト関係)に掲げてい
たら、次のようなアドバイスを受けた。
48=6×8(適当な2つの数の積!)より、まず6山でのシャッフルをする。
その後、8山でのシャッフルをすれば、必ず逆順復元が起きている。
この操作(6山シャッフル→8山シャッフル)をもう一度行うと、正順に復元される。
いちいち枚数に従った復元回数を覚えなくても、いいわけだ。山の数を変更してシャッ
フルする発想がすばらしい。カードマジックの創作に大いに利用できそうだ。
GAI さんが言われる操作を実際に行ってみた。
まず、6山シャッフルすると、
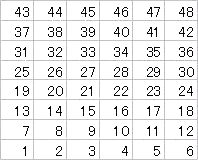
次に、8山シャッフルすると、

(コメント) お〜!確かに、2回のシャッフルで逆順に並んでしまいましたね!