
�@���g�o�����������b�ɂȂ��Ă���g�m�u�您�����v����̏o��ł��B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�����Q�S�N�T���Q�T���t���j
�@ cos24߁{cos48߁{cos72߁{cos96߁{cos120߁{cos144߁{cos168�
�@�̒l�����߂�B
�i���j�@-1/2
�@�您��������̉������Ă����܂��B�a��ςɂȂ����������A
�@�@cos48߁{cos72߁�2cos{(48߁{72�)/2}cos{(48�-72�)/2}
�@�@��2cos60�cos(-12�)��cos12�
�@�@cos96߁{cos144߁�2cos{(96߁{144�)/2}cos{(96�-144�)/2}
�@�@��2cos120�cos(-24�)��-cos24�
�@�܂��A�@cos168߁�cos(180�-12�)��-cos12�
�@�@����āA
�@�^����cos24߁{cos12߁{cos120߁{(-cos24�)�{(-cos12�)
�@�@�@�@��cos120߁�-1/2
�@�U���@����̃R�����g�ł��B�i�����Q�S�N�T���Q�U���t���j
�@��=24߁A48߁A96߁A120߁A168� �̂Ƃ��A
�@�@5��=120߁A240߁A480�(=360�+120�)�A600�(=360�+240�)�A840�(=720�+120�) �Ȃ̂ŁA
cos5��=-1/2 �����A�@16cos5��-20cos3��+5cos��=-1/2�@�����B�i���@�Q�l�j
����āAcos24߁Acos48߁Acos96߁Acos120߁Acos168� �́A32��5-40��3+10��+1=0 �̉��ƂȂ�B
���ׂĈقȂ邩��A���̘a�́A���ƌW���̊W�ɂ��A0
�@�܂��A��=72߁A144� �̂Ƃ��Acos5��=1 �����̂ŁA�@16cos5��-20cos3��+5cos��=1
����āA cos72߁Acos144� �́A16��5-20��3+5��-1=0�@�����A�@(��-1)(4��2+2��-1)2=0�@�̉�
����1�@�Ȃ̂ŁA�@4��2+2��-1=0�@�̉��ƂȂ�B���̘a�́A���ƌW���̊W�ɂ��A-1/2
���������āA
�@cos24߁{cos48߁{cos72߁{cos96߁{cos120߁{cos144߁{cos168�=0+(-1/2)=-1/2
�i�Q�l�j�@��[k=1,n]cosk��
�@�@�@�@�@=-1/2�@��=��/(n+1/2)�̂Ƃ�
�@�@�@�@�@=-1�@�@ ��=��/n�̂Ƃ�
�@�@�@�@�@=0 �@�@ ��=��/(n+1)�̂Ƃ�
�ޑ��@�@cos24�cos48�cos72�cos96�cos120�cos144�cos168߁@�̒l�����߂�B
�i���j�@(-1/32)(-1/4)=1/128
�ޑ��@�@cos12�cos24�cos36�cos48�cos60�cos72�cos84߁@�̒l�����߂�B
�i���j�@cos12�cos24�cos36�cos48�cos60�cos72�cos84�
�@�@�@={-cos(180�-12�)}cos24�{-cos(180�-36�)}cos48�cos60�cos72�{-cos(180�-84�)}
�@�@�@={-cos168�}cos24�{-cos144�}cos48�cos60�cos72�{-cos96�}
�@�@�@={ cos24�cos48�cos72�cos96�cos144�cos168�} (-1) cos60�
�@�@�@={ cos24�cos48�cos72�cos96�cos144�cos168�} (-1/2)
�@�@�@={ cos24�cos48�cos72�cos96�cos144�cos168�} cos120�
�@�@�@=cos24�cos48�cos72�cos96�cos120�cos144�cos168�
�@�@�@=1/128
�i�ʉ��j�@sin2��=2sin��cos�Ƃ��A
�@�@2(cos12�)=(sin24�)/(sin12�)�@�A2(cos24�)=(sin48�)/(sin24�)�@�A2(cos36�)=(sin72�)/(sin36�)
�@�@2(cos48�)=(sin96�)/(sin48�)={sin(180�-96�)}/(sin48�)=(sin84�)/(sin48�)�@�A2(cos60�)=1
�@�@2(cos72�)=(sin144�)/(sin72�)=(sin36�)/(sin72�)�@�A
�@�@2(cos84�)=(sin168�)/(sin84�)=(sin12�)/(sin84�)
�@�ӁX�����āA27�~(�^��)=1�@���A�@�^��=1/128
�i�R�����g�j�@�U���@����̉́A�G���K���g�ł��ˁI
�@�您��������̃R�����g�ł��B�i�����Q�S�N�T���Q�U���t���j
�@�U���@����A���肪�Ƃ��������܂��B�X�ɂ́A�ς̖����o���Ă��������āE�E�E�B���ƌW����
�̊W���g������@���������Ƃ͒m��܂���ł����B
�@�炢����̃R�����g�ł��B�i�����Q�S�N�T���Q�U���t���j
�@�U���@����́i�Q�l�j�ɂ��āA�����炭���������낤�Ǝv���̂ŋ��k�ł����A��̓I�ɂ�
�@��[k=1,n]cosk��= sin(n+1/2)��/2sin(��/2)-1/2= (sin(n+1)��+sin(n��))/2sin��-1/2
�ƂȂ�܂��ˁB
�@�您��������̃R�����g�ł��B�i�����Q�S�N�T���Q�V���t���j
�@���̖��́A��w�ւ̐��w ��Έ�Ή��̉��K ���w�U��70�y�[�W�ɍڂ��Ă������ł��B
�ł����A���N��萔�w�T�AA�◝�Ȃ��V�͈͂ɂȂ����̂ŁA�V�͈͂̐��w�U�ł����̖�肪
�Љ��邩������Ȃ��̂ōw�����ꂽ�����͂����߂ɁE�E�E
�@�ۂ��ۂ���̃R�����g�ł��B�i�����Q�S�N�T���Q�V���t���j
�@���̖���}�`�I�ɍl���Ă݂܂����B
�@���p�`�� 12� �ł���ӎO�p�`�`�a�b�̕ӂ`�a��� �o1�A�o2�A�o3 ���A�ӂ`�b��ɂp1�A�p2�A
�p3���A�@�`�o1���o1�p1���p1�o2���o2�p2���p2�o3���o3�p3���p3�a���a�b��1�@�ɂȂ�悤�ɂƂ邱
�Ƃ��l����B
�@�@
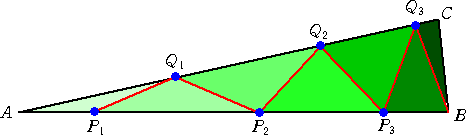
�@���̂Ƃ��A
�@�@�`�a���`�o1+�o1�o2+�o2�o3+�o3�a��1+2cos24߁{2cos48߁{2cos72�
�@�@�`�b���`�p1+�p1�p2+�p2�p3+�p3�b��2cos12߁{2cos36߁{2cos60�+2cos84�
�@�@�@�@��-2cos168�-2cos144�-2cos120�-2cos96�
�@AB=AC���A�@1+2cos24߁{2cos48߁{2cos72߁�-2cos168�-2cos144�-2cos120�-2cos96�
�@�@1+2cos24߁{2cos48߁{2cos72�+2cos96�+2cos120�+2cos144�+2cos168߁�0
�@����āA�@cos24߁{cos48߁{cos72�+cos96�+cos120�+2cos144�+2cos168߁�-1/2
�@���ς̕��́A��30�p�`�̈�_����o��Ίp���̒����̐ςƐ�15�p�`�̑Ίp���̒�����
�@�@�ς��l����A�}�`�I�ɉ�����悤�ł��B
�@�您��������̃R�����g�ł��B�i�����Q�S�N�T���Q�V���t���j
�@�ۂ��ۂ���A�炢����A���肪�Ƃ��������܂��B�����͐����p�`���������Ƃ͎v������
�������̂ŁE�E�E
�@�炢�����U���@����̏Љ�������g���ƁA�ȉ��̂悤�ɂ��ł��܂��B
�@�@��[1,n]cosk�Ɓ�(sin(n+1/2)��/2sin(��/2))-1/2�@�ł��邩��A�^���́An��7�Ƃ����Ƃ���
�@�Ɓ�24߂ɓ������B����āA
�@cos24߁{cos48߁{�E�E�E�{cos168߁���[1,7]cos24�k��(sin180�/sin12�)-1/2��0-1/2��-1/2