
当HPがいつもお世話になっているHN「GAI」さんからの出題です。(平成21年9月15日)
さいころが9個(3×3)入る箱があり、中央にはさいころがなく、周りに8個のさいころが 1
の目を下にして配置されている。
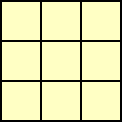
さいころを空き地に転がすことで、全てのさいころの目が 1 が出現して終了するようにし
たい。そのためには何手必要だろうか?
(一見不可能に感じられますが、実は可能な手順が構成できます。1ヶ月は楽しめます。貴
方の挑戦を待ちます。)
(答) この1ヶ月は楽しめるかも...という問題に、らすかるさんは果敢に挑戦され、出題
後、わずか3時間弱で解かれたようだ。(平成21年9月15日)...スゴイですね!
らすかるさんからのコメント: 1ヶ月は楽しめませんでしたが(笑)、なかなか面白い問
題でした。私が見つけた手順は、150手ですが、まず間違
いなく、最小手数ではないと思います。でも、とても簡単な
手順で、覚えやすいです。最小手数は全然わかりません
が、とても20手以下とは思えませんのでコンピュータで全
数探索を行って調べるのも無理ですね。
これに対して、出題者のGAIさんによれば、最少手数は36手ではないかとのこと。
(平成21年10月3日付け)
平成21年10月4日付けで、らすかるさんがプログラムを作って調べたところ、36手が最
少手数で、解は、次のようになるとのことである。(ただし、対称形はすべて削除)
中心空き他全部裏→中心空き他全部表 : 36手、1通り
↓←↑→↓→↑←↑→↓←↑←↓↓→↑→↓←↑←↓→↑→↓←←↑→→↑←↓
また、上記の解は「終了時に真ん中のマスが空き」という条件で調べているが、最終形を
「中心のマスが空き」に限定しない場合は次の34手が最短とのこと。
(ただし、対称形はすべて削除)
中心空き他全部裏→空き位置問わず全部表 : 34手、3通り
↓←↑↑→↓←↓→↑←↓→↑→↑←←↓→↓→↑←↑←↓↓→↑←↑→→
↓←↑↑→↓←↓→↑→↑←↓←↓→→↑←↑←↓→↑←↓↓→↑←↑→→
↓←↑↑→↓→↑←↓←↓→↑←↓→→↑←↑←↓→↑←↓↓→↑←↑→→
らすかるさんによれば、個人的には、最終形は「中心のマスが空き」に限定した方がきれ
いだと思うとのことである。(平成21年10月4日付け)
また、GAIさんより、この問題の別バージョンが提示された。(平成21年10月4日付け)
さいころの「1」の目をすべて手前側に向けてからスタートして、最後には上面がすべて
「1」の目に揃えるには何手必要か?
これに対しても、らすかるさんは直ぐ解決された。(平成21年10月4日付け)
新しいプログラムを作り、最短手順を全通り調べたとのこと。
(ただし、対称形はすべて削除)
中心空き他全部手前向き→中心空き他全部表 : 36手、10通り
←↑→→↓←←↓→↑↑→↓↓←↑→↓←↑←↓→↑←↑→↓→↑←↓→↓←↑
←↑→↓←↓→↑→↓←↑←↓→↑↑←↓→→↓←←↑↑→↓←↑→↓→↑←↓
←↓→↑←↑→→↓↓←↑→↑←←↓↓→↑←↑→↓←↓→→↑↑←↓←↑→↓
←↓→↑←↑→↓←↓→↑←↓→↑→↓←↑→↑←↓←↑→↓←↑→↓←↑→↓
←↓→↑←↑→↓←↓→↑←↓→↑→↓←↑→↑←↓←↑→↓→↑←↓→↑←↓
←↓→↑←↓→↑←↑→↓→↑←←↓→→↓←←↑→→↑←↓←↑→↓→↑←↓
←↓→↑←↓→↑←↑→↓→↑←←↓→→↓←↑→↑←↓↓←↑↑→↓→↑←↓
←↓→↑←↓→↑←↑→↓→↑←←↓→→↑←↓→↓←←↑→→↑←↓←↑→↓
←↓→↑←↓→↑←↑→↓→↑←←↓→→↑←↓→↓←↑→↑←↓↓←↑↑→↓
↑←↓→↑←↓↓→↑←↓→↑←↓→↑→↓←↑→↓←↑←↓→→↑↑←←↓→
中心空き他全部前向き→空き位置問わず全部表 : 27手、1通り
←↓→↑←↑→↓←↓→↑←↓→↑→↓←↑→↑←↓←↑→
(注意) 「対称形はすべて削除」において、左右対称、上下対称、回転対称の他に、「全部
裏」を「全部表」にする場合は、“前後対称”(手順を逆順にして同じになるもの)も除
いている。
最終形の空きマス位置を中心に限定すると両方とも最短36手で、空きマス位置を限定し
ない場合は全部前向きの方が少ない手数でできる。
GAIさんは、「最初さいころを同じ向きにセットしておけば、36手ですべて上面がどんな数
字でも揃えることが可能なんですね。平面ルービックキューブと命名しましょう。」と提案され
た。(平成21年10月4日付け)
らすかるさんからの続報です。(平成21年10月11日付け)
最初の状態が、 「中心空き他全部裏」 、 「中心空き他全部手前向き」 のどちら
であっても、「中心空き他全部表」(以下、この状態を「基本形」と呼ぶことにする。)までの
最短手数は、36手であった。こういう結果になると、
「もしかして、どんなパターンでも36手以内?」
なんて考えが浮かんで調べたくなり、しばらくこの問題を研究していました。
そこで、9×9のマス目のうち空きの可能性が9通りで、そのうちの1通りに対して、8個の
さいころの目の出方が68通りあるので、全パターン数は、9×68=15116544通りとなる。
このうち、36手以内で基本形まで到達できるパターン数を調べたところ、14029322通り
であった。(即ち、全体の92.8%は36手以内で基本形に到達できる!)
こうなると、今度は、
「どんなパターンでも、n 手以内で基本形に到達できる」
を満たす n の最小値を調べたくなって、その結果は、49手であった。
(49手の全パターンを調べるのに、50時間かかりました。)
n 手以内で基本形に到達できるパターンの数は、以下の通り。