菱餅詰め　　　 　　　　 　　　　　　　　 　　　　　　　　　　　　　　　

　当ＨＰがいつもお世話になっているＨＮ「ＧＡＩ」さんからの出題です。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（令和３年６月６日付け）

　一辺が1の正六角形に、一辺が1の正三角形を2つ継ぎ合わせた菱形(diamondと呼ぶこと
にする)を3個用いて埋めつくすことをすれば、下図のfig1、fig2 が考えられる。

<fig1>		<fig2>

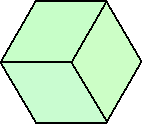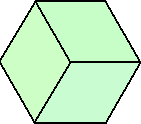　但し、この2つは180°の回転で同一型だから、本質的に1タイプしか入れ方が起こらない。

　そこで今度は、

(1)　一辺が2の正六角形に12(=3*2^2)個のdiamonds(一辺は1の菱形) を埋め尽くす型は、
　　回転や鏡像で同じになるものは一つと数えると何通り可能か？

(2)　同じく一辺が3の正六角形の場合は27(=3*3^2)個のdiamodsを埋めることになるが、何
　　通り可能か？
















































（答）　らすかるさんが考察されました。（令和３年６月６日付け）

　「A066931」がその答えで合っていれば、(1)は、6通り、(2)は、113通り


　ＧＡＩさんからのコメントです。（令和３年６月６日付け）

　よく探し出せましたね。これを出した経緯がすごく複雑で、しかし、計算可能であることに驚
いて、出題していました。

　らすかるさんの手法は？この113通りはプログラムで作り出せるんですか？

　6通りは何とか手作業で見つけました。


　らすかるさんからのコメントです。（令和３年６月６日付け）

　 この113通りはプログラムで作り出せるんですか？

　プログラムは作れば作れますが、実行時間がかなりかかりそうな気がして、その後の高速
化作業など考えると結構手間がかかりそうなので、やめました。

　6通りは何とか手作業で見つけました。

　私も、6通りは手作業で見つけました。

　(2)も途中までは手作業でやったのですが（多分全体の1/5ぐらい）、結構大変なうえ結果が
正しいかどうかも怪しいので諦めました。

　らすかるさんの手法は？

　OEISで「1,6 hexagon diamond tiling」を検索したら2番目にありました。


（コメント）　（１）の６通りは手作業で求められるということで、私も挑戦してみました。

　出来た立体をジ〜ッと眺めていると、一つの立体が多様に見えてくるのが不思議な感覚
です！

　　　　　　　


　　　　　　　


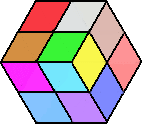
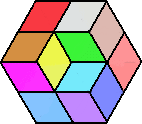
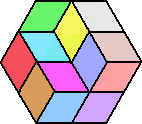
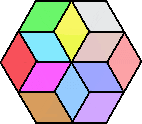
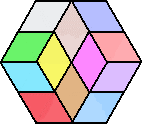
　後で考えてみると、２×２の立方体から、１×１の立方体を取り除いていく場合に対応して
いるんですね！

＃　令和３年６月１０日付けで、当ＨＰがいつもお世話になっているＨＮ「ＰＢ」さんから、上記
　の図に回転して同じものになるものがある旨、ご指摘いただきました。上図は修正済みで
　す。ＰＢさんに感謝します。


　moonlight さんからのコメントです。（令和３年６月１７日付け）

　バタバタしていて見逃していました。菱餅詰めは、

　「小さな立方体をその何倍かのサイズの立方体の中に奥から詰めて置く」

事に対応するのではないのかと...。（まだちゃんと考えてないので思いつきですけど）


　らすかるさんからのコメントです。（令和３年６月１７日付け）

　対応すると思います。ただし、120/240°回転、線対称反転、そして前後重複（例えば、1
個置いたのと、n^3-1個置いたのが同じ図形になる）により、一対多対応になりますので、
そこをうまく計算できるかどうかですね。
（それよりも「奥から詰める」方が数えるのが大変かも知れません）