比の利用　　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　　

　当ＨＰがいつもお世話になっているＨＮ「よおすけ」さんからの出題です。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（平成２６年１月８日付け）

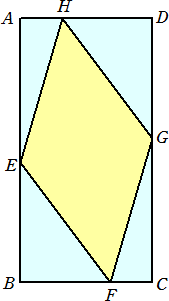平面上に、AB：BC=2：1 の長方形ABCDがあり、その内部 　　　に、一辺が25cmのひし形が接する。AB、BC、CD、DA との 　　　それぞれの接点をE、F、G、Hとする。 　　　　AE：EB=6：5、EF：EB=5：4 のとき、AB、BCの長さを求めよ。

（答）　ＡＢ＝４４ｃｍ　、ＢＣ＝２２ｃｍ

　実際に、EF：EB＝５：４で、ＥＦ＝２５　より、ＥＢ＝２０、ＢＦ＝１５　である。AE：EB＝６：５

　より、ＡＥ＝２４、ＡＨ＝７　となるので、ＡＢ＝２４＋２０＝４４（ｃｍ）

　また、ＦＣ＝ＡＨ　より、ＦＣ＝７　なので、　ＢＣ＝１５＋７＝２２（ｃｍ）