当HPがいつもお世話になっているHN「GAI」さんからの出題です。
(平成25年12月22日付け)
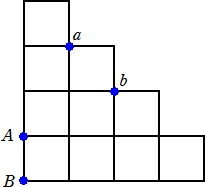
Aとa、Bとb、Cとcをお互いに交差しない(点で重ならないことも含む)配線の系は何通りあ
るでしょう。
ただし、線の引き方は下図の線に沿って、横か縦に遠回りにならないように配線するもの
とする。
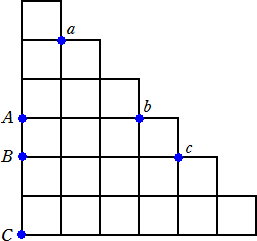
(答) らすかるさんが考察されました。(平成25年12月22日付け)
ごく普通の解き方ですが…
(1) B→b が「右上右右」の場合
A→aは、「上右上」「上上右」の2通り
C→cは、「右右」の地点を通らない場合、「右右上」の地点までが、2C1=2通り、その先が
3C1=3通りなので、2×3=6通り
「右右」の地点を通る場合、「右右」の地点までは1通り、その先が、4C2=6通り
合計12通りなので、全部で、2×12=24通り
(2) B→b が「右右上右」の場合
A→aは、3C2=3通り
C→cは、「右右右」の地点を通らない場合、「右右右上」の地点までが、3C1=3通り、その
先が、2C1=2通りなので、3×2=6通り
「右右右」の地点を通る場合、「右右右」の地点までは1通り、その先が、3C2=3通り
合計9通りなので、全部で、3×9=27通り
(3) B→b が「右右右上」の場合
A→aは、3C2=3通り
C→cは 5C1=5通り
よって、全部で、3×5=15通り
以上合計して、24+27+15=66通り
GAI さんからのコメントです。(平成25年12月22日付け)
らすかるさん、正解です。これを次のように計算できるのに感動しました。
A、B、Cの位置を上から数えると、3、4、6。 また、a、b、cの位置が、1、3、4に対応する。
そこで、A→a、A→b、A→c への道の取り方がそれぞれ、3C1、3C3、3C4 即ち、3、1、0
同様に、B→a、B→b、B→c への道の取り方がそれぞれ、4C1、4C3、4C4 即ち、4、4、1
C→a、C→b、C→c への道の取り方がそれぞれ、6C1、6C3、6C4 即ち、6、20、15
このとき、3×3行列
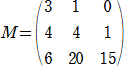
を作り、その行列式を求めると、
det(M)=3*4*15+1*1*6+4*20*0-0*4*6-1*4*15-3*20*1=66
行列式の意味を図形に関連づけるアイデアに感服しました。
(コメント) GAI さんの行列を用いた別解がとても不思議だったので、別な問題で試してみ
ました。