
下図のような空所がある。
|
|
この空所に、数字の1から5までが順に並んでいる。
|
これらの数字を、次のルールに従って並べ替える。
(ルール) 1. 1→2→3→4→5→1→2→・・・ と数字の順番に、数字を、数字の入って
いない空所のどちらかに移動する。
2. 1回の操作で動かせる数字は、ひとつだけとする。
このとき、次のように数字を並べ替えるには、最低何回の操作が必要であろうか?
|
Flash で、数字を実際に動かしてみよう。
Flash 版は、こちら HTML 版は、こちら をクリックしてください。
セキュリティ保護のため、コンピュータにアクセスできるアクティブ コンテンツが表示されないように、
Internet Explorer で制限していると、HTML版、Flash版ともに見られません。ブロックされている
コンテンツを許可してください。(すみません、自己の責任でお願いします。)
(答) 13回の操作で出来る。次のように並べ替えればよい。
|
当HPがいつもお世話になっているHN「FN」さんが、このパズルを次のように拡張された。
(平成22年6月26日付け)
下図のような空所がある。
|
|
この空所に、数字の1から6までが順に並んでいる。
|
これらの数字を、次のルールに従って並べ替える。
(ルール) 1. 1→2→3→4→5→6→1→2→・・・ と数字の順番に、数字を、数字の入
っていない空所のどちらかに移動する。
2. 1回の操作で動かせる数字は、ひとつだけとする。
このとき、次のように数字を並べ替えるには、最低何回の操作が必要であろうか?
|
この問題について、当HPがいつもお世話になっているHN「らすかる」さんが、数字が幾つ
あっても解があることを次のように示された。(平成22年6月26日付け)
以下で、空所を数字の「0」で表すことにする。
(1)数字の個数が偶数個の場合
たとえば、 「00123456」について、「1」と「2」を入れ替える操作
12345600 ← 1〜6まで2マスずらす
34560012 ← 1と2は6マス、3〜6まで2マスずらす
56001234 ← 1と2は2マス、3と4は6マス、5と6は2マスずらす
00213456 ← 1を1マス、2を3マス、3と4は2マス、5と6は6マスずらす
(2)数字の個数が奇数個の場合
たとえば、 「0012345」について、「1」と「2」を入れ替える操作
1234500 ← 1〜5まで2マスずらす
3450012 ← 1と2は5マス、3〜5まで2マスずらす
4500123 ← 1と2は1マス、3は5マス、4と5は1マスずらす
0021345 ← 1を1マス、2を3マス、3は2マス、4と5は5マスずらす
上記のようにすれば、任意の2マスを入れ替えることが出来るので、必ず解にたどり着く
ことができる。
(コメント) なるほど、合点!
さらに、らすかるさんは、n≦11 の最短手数も調べられた。
| 数字の個数(n) | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 最短手数 | 3 | 5 | 6 | 13 | 21 | 25 | 28 | 41 | 55 | 61 |
らすかるさんによれば、この数列は数列サイトにはなく、増加数列かどうかも分からない
とのこと。
上記の範囲では、 (最短手数)=n(n+1)/2−A
ただし、n が奇素数のとき、 A=(n−1)/2
n が指数 k の累乗数のとき、 A=4(k−1) あるいは A=2k
その他の場合、 A=0
が成り立っているが、この先も成り立つかどうかはまったく不明とのことである。
(コメント) n=6 のときの最短手数が「21手」とのことなので、挑戦してみました!
|
このような機会を与えていただいた、らすかるさんに感謝します。
当HPがいつもお世話になっているHN「GAI」さんが、n=5、6、7
の場合について、手順
を示された。(平成22年6月27日付け)
| n=5 手数 状 態 数字 空席の 0 0012345 1 左へ 1 1002345 2 左 2 1200345 3 右 3 1203045 4 左 4 1243005 5 左 5 1243500 1 左 6 0243510 2 左 7 2043510 3 左 8 2340510 4 左 9 2304510 5 左 10 2354010 1 右 11 2354001 2 右 12 0354021 3 右 13 0054321 |
n=6 手数 状 態 数字 空席の 0 00123456 1 左へ 1 10023456 2 左 2 12003456 3 右 3 12030456 4 左 4 12430056 5 左 5 12435006 6 右 6 12435060 1 左 7 02435160 2 左 8 20435160 3 左 9 23405160 4 左 10 23045160 5 左 11 23540160 6 右 12 23540106 1 右 13 23540016 2 右 14 03540216 3 左 15 30540216 4 右 16 30504216 5 右 17 30054216 6 右 18 30654210 1 右 19 30654201 2 右 20 30654021 3 右 21 00654321 |
n=7 手数 状 態 数字 空席の 0 001234567 1 左へ 1 100234567 2 左 2 120034567 3 左 3 123004567 4 左 4 123400567 5 左 5 123450067 6 左 6 123456007 7 右 7 123456070 1 左 8 023456170 2 左 9 203456170 3 左 10 230456170 4 左 11 234056170 5 左 12 234506170 6 右 13 234500176 7 右 14 234507106 1 右 15 234507016 2 右 16 034507216 3 左 17 304507216 4 左 18 340507216 5 右 19 340057216 6 右 20 340657210 7 左 21 347650210 1 右 22 347650201 2 右 23 347650021 3 右 24 047650321 4 右 25 007654321 |
(コメント) GAI さん、ありがとうございます。n=6 の場合について、私のものと微妙に違
うので、解も一通りには決まらないことが分かりました!(当たり前かな...?)
この問題に関連して、FNさんが新しい記法を考えられた。(平成22年6月28日付け)
1から順に、2、3、・・・、n を移動する n 手をまとめて、1巡と呼ぶことにし、局面AからB
に1巡で移ることを、「 A⇒B 」で、1手で移るのを、「 A→B 」で書くことにする。
n=2、3、4、5、6、7 の手順の1つを、この記法で書いてみると次のようになる。
n=2 0012 ⇒ 0120 → 0021
n=3 00123 ⇒ 12300 →→ 00321
n=4 001234 ⇒ 124300 →→ 004321
n=5 0012345 ⇒ 1243500 ⇒ 2354010 →→→ 0054321
n=6 00123456 ⇒ 12435060 ⇒ 23540106 ⇒ 30654210 →→→ 00654321
n=7 001234567 ⇒ 123456070 ⇒ 234507106 ⇒ 347650210 →→→→ 007654321
らすかるさんより、n=8 のときの手順を頂いた。(平成22年6月28日付け)
0012345678 ⇒ 1235460780 ⇒ 2376501804 ⇒ 3487652010 →→→→ 0087654321
(コメント) FNさんの記法で見通しよくなりましたネ!
GAI さんが、「根性?」で、n=9 のときの手順を導かれた。(平成22年6月29日付け)
n=9 00123456789 ⇒ 12354607890 ⇒ 23765018904
⇒ 34876520019 ⇒ 45987632100 →→→→→ 00987654321
さらに、らすかるさんが、n=10、11、12 の手順を導かれた。(平成22年6月29日付け)
n=10
00123456789A ⇒
1235406789A0 ⇒
237651089A04 ⇒
3487621900A5 ⇒
45987630210A ⇒
50A987643210 →→→→→
00A987654321
n=11
00123456789AB ⇒
123546B789A00 ⇒
234657090AB81 ⇒
3457602A1B098 ⇒
45698730201AB ⇒
56BA987143200 →→→→→→
00BA987654321
n=12
00123456789ABC ⇒
1234657C89AB00 ⇒
234576A090BC18 ⇒
34568702A1C09B ⇒
45A798630201BC ⇒
56CBA987143200 →→→→→→
00CBA987654321
らすかるさんによれば、n=12の場合に66手が最短であることが証明できたとのこと。
(平成22年6月30日付け)
(証明) もし、n=12が、65手で出来たとすると、
00123456789ABC⇒
QRXXXXSTUVWXYZ⇒
QRXXXXSTUVWXYZ⇒
QRXXXXSTUVWXYZ⇒
QRXXXXSTUVWXYZ⇒
MNCBA9876PXXL0+5手
の形になる。(L、M、N、P〜Zは以降の説明のための記号である)
M、Nは5以下なので、M、N、Q、Rの範囲内に少なくとも一つの0がなければならない。
また、P≠0 のとき、S〜Zの各列には少なくとも一つの0が必要である。
P≠0 のとき
2行目〜5行目に存在する0の個数は8個なので、S〜Zの各列にちょうど一つずつの
0が必要。Q、Rは0に出来ないので、MかNのいずれかが0である。
すると、Lは1と決まるので、Yの中にもう一つ0が必要となるが、それは不可能。
P=0 のとき
M、Nは0に出来ないので、QかRのうち少なくとも一つに0が入る。
また、S〜U、W〜Zにそれぞれ0が少なくとも一つ必要であるが、Lは1なので、Yには
0が少なくとも2つ必要となる。このとき、2行目〜5行目に0が9個必要となり、不可能。
61手〜64手は、6行目のPXXLの部分が固定されるだけなので出来ない。
60手は、S〜Zの範囲に0が10個必要となって不可能。
59手は、
00123456789ABC⇒
XXXXXXSTUVWXYZ⇒
XXXXXXSTUVWXYZ⇒
XXXXXXSTUVWXYZ⇒
XXCXXXSTUVWXYZ+11手
のようになるが、5行目は右から順に、0、1以下、2以下、…、A以下でなければならな
いことを考慮すると、S〜Zの範囲に0が少なくとも10個必要となり、不可能。
同様に、58手以下も不可能となり、結局66手が最短となる。 (証終)
これまでの最短手数をまとめると、
| 数字の個数(n) | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 最短手数 | 3 | 5 | 6 | 13 | 21 | 25 | 28 | 41 | 55 | 61 | 66 |
となる。
FNさんやらすかるさんの探究の結果、上記の範囲では、
n が奇数のとき、 (最短手数)=(n2+1)/2
(実際に、 n=3 → (最短手数)=5 、n=5 → (最短手数)=13 、
n=7 → (最短手数)=25 、n=9 → (最短手数)=41 、
n=11 → (最短手数)=61 、 ・・・・・・・・ )
※ FNさんによれば、「1〜n を動かす操作を(n−1)/2回行って、後ろの(n−1)/2
個を正しい位置に入れ、前の(n+1)/2個を最後に入れて完成」ということで、
(n−1)/2×n+(n+1)/2=(n2+1)/2
が導かれるとのこと。(平成22年6月27日付け)
n=4k (k=1、2、3、・・・)のとき、 (最短手数)=n(n−1)/2
(実際に、 n=4 → (最短手数)=6 、n=8 → (最短手数)=28 、
n=12 → (最短手数)=66 、 ・・・・・・・・ )
n=4k+2 (k=0、1、2、・・・)のとき、 (最短手数)=n(n+1)/2
(実際に、 n=2 → (最短手数)=3 、n=6 → (最短手数)=21 、
n=10 → (最短手数)=55 、 ・・・・・・・・ )
が成り立っている。(n≧13 についても成り立つかどうかは不明!)
らすかるさんによれば、一般に、
n が奇数のとき、 (n2+1)/2 手未満では不可能
n=4k (k=1、2、3、・・・)のとき、 n(n−1)/2 手未満では不可能
n=4k+2 (k=0、1、2、・・・)のとき、 n(n+1)/2 手未満では不可能
ということが証明されたとのことである。(平成22年6月30日付け)
(証明) n=4k の場合(行数は、2k、列数は、4k+2)
2行目〜2k行目(つまり、2行目以降全部)の範囲において、1列目〜2列目(下図Rの
範囲)で少なくとも1個、k+4列目〜3k+3列目(下図Sの範囲)は各列少なくとも1個ず
つ、3k+4列目〜4k+2列目(下図Tの範囲)は各列少なくとも2個ずつなので、合計す
ると、最小 1+2k+2(k−1)=4k−1個となるが、2行目〜2k行目の0の個数は、
4k−2個なので矛盾。
(k=4 の場合の参考図)
00123456789ABCDEFG⇒
RRXXXXXSSSSSSSSTTT⇒
RRXXXXXSSSSSSSSTTT⇒
RRXXXXXSSSSSSSSTTT⇒
RRXXXXXSSSSSSSSTTT⇒
RRXXXXXSSSSSSSSTTT⇒
RRXXXXXSSSSSSSSTTT⇒
RRGFEDCBA98SSSSTTT+0〜7手
n=4k+1 の場合(行数は、2k+1、列数は、4k+3)
2行目〜2k+1行目(つまり、2行目以降全部)の範囲において、
(1) 2k巡+k〜2k手で出来ないことの証明
1列目〜2列目(下図Rの範囲)で少なくとも1個、k+4列目〜3k+3列目(下図Sの
範囲)は各列少なくとも1個ずつ、3k+4列目〜4k+3列目(下図Tの範囲)は各列少
なくとも2個ずつなので、合計すると、最小 1+2k+2k=4k+1個となるが、2行目〜
2k+1行目の0の個数は4k個なので矛盾。
(k=4 の場合の参考図)
00123456789ABCDEFGH⇒
RRXXXXXSSSSSSSSTTTT⇒
RRXXXXXSSSSSSSSTTTT⇒
RRXXXXXSSSSSSSSTTTT⇒
RRXXXXXSSSSSSSSTTTT⇒
RRXXXXXSSSSSSSSTTTT⇒
RRXXXXXSSSSSSSSTTTT⇒
RRXXXXXSSSSSSSSTTTT⇒
RRHGFEDCBA9SSSSTTTT+4〜8手
(2) 2k巡+0〜k−1手で出来ないことの証明
1列目〜2列目(下図Rの範囲)で“各列”少なくとも1個、k+4列目〜3k+4列目(下
図Sの範囲)は各列少なくとも1個ずつ、3k+5列目〜4k+3列目(下図Tの範囲)は各
列少なくとも2個ずつなので、合計すると、最小 2+(2k+1)+2(k−1)=4k+1個
となるが、2行目〜2k+1行目の0の個数は4k個なので矛盾。
(k=4 の場合の参考図)
00123456789ABCDEFGH⇒
RRXXXXXSSSSSSSSSTTT⇒
RRXXXXXSSSSSSSSSTTT⇒
RRXXXXXSSSSSSSSSTTT⇒
RRXXXXXSSSSSSSSSTTT⇒
RRXXXXXSSSSSSSSSTTT⇒
RRXXXXXSSSSSSSSSTTT⇒
RRXXXXXSSSSSSSSSTTT⇒
RRHGFEDCBA987654TTT+0〜3手
n=4k+2 の場合(行数は、2k+2、列数は、4k+4)
2行目〜2k+2行目(つまり2行目以降全部)の範囲において、1列目〜2列目(下図R
の範囲)で“各列”少なくとも1個ずつ、k+4列目〜3k+4列目(下図Sの範囲)は各列少
なくとも1個ずつ、3k+5列目〜4k+4列目(下図Tの範囲)は各列少なくとも2個ずつな
ので、合計すると、最小 2+(2k+1)+2k=4k+3個となるが、2行目〜2k+2行目
の0の個数は4k+2個なので矛盾。
(k=4 の場合の参考図)
00123456789ABCDEFGHI⇒
RRXXXXXSSSSSSSSSTTTT⇒
RRXXXXXSSSSSSSSSTTTT⇒
RRXXXXXSSSSSSSSSTTTT⇒
RRXXXXXSSSSSSSSSTTTT⇒
RRXXXXXSSSSSSSSSTTTT⇒
RRXXXXXSSSSSSSSSTTTT⇒
RRXXXXXSSSSSSSSSTTTT⇒
RRXXXXXSSSSSSSSSTTTT⇒
RRIHGFEDCBA9SSSSTTTT+0〜8手
n=4k+3 の場合(行数は、2k+2、列数は、4k+5)
2行目〜2k+2行目(つまり2行目以降全部)の範囲において、1列目〜2列目(下図R
の範囲)で少なくとも1個、k+4列目〜3k+5列目(下図Sの範囲)は各列少なくとも1個
ずつ、3k+6列目〜4k+5列目(下図Tの範囲)は各列少なくとも2個ずつなので、合計
すると、最小 1+(2k+2)+2k=4k+3個となるが、2行目〜2k+2行目の0の個数
は4k+2個なので矛盾。
(k=4 の場合の参考図)
00123456789ABCDEFGHIJ⇒
RRXXXXXSSSSSSSSSSTTTT⇒
RRXXXXXSSSSSSSSSSTTTT⇒
RRXXXXXSSSSSSSSSSTTTT⇒
RRXXXXXSSSSSSSSSSTTTT⇒
RRXXXXXSSSSSSSSSSTTTT⇒
RRXXXXXSSSSSSSSSSTTTT⇒
RRXXXXXSSSSSSSSSSTTTT⇒
RRXXXXXSSSSSSSSSSTTTT⇒
RRJIHGFEDCBASSSSSTTTT+0〜9手
(証終)
FNさんが、らすかるさんの証明を参考にして、n=13のときの証明を、n=2k+1への一
般化を意識しながら試みられた。(平成22年6月30日付け)
n=13のとき、6巡+6手以下では不可能であることの証明
6巡+1〜6手で可能であるとする。
00123456789ABCD⇒
RRXXXXSSSSSSSSS⇒
RRXXXXSSSSSSSSS⇒
RRXXXXSSSSSSSSS⇒
RRXXXXSSSSSSSSS⇒
RRXXXXSSSSSSSSS⇒
MMDCBA987JJJKL0+1〜6手
まず、6巡が終わった後、6手以内で完成するために、7以上は正しい位置に入っていなけ
ればならないから、最終行の「DCBA987」は確定する。
また、次の手で、「1」が正しい位置(最後)に入るために、最右端は「0」である。
当然ながら、最終行の「DCBA987」以外は、「6」以下である。
各行に、「0」が2つあるが、それを除いて各数は1つ上の数より大きい。
(1から順に置いていくから、1は0の下しか置けないし、2は0か1の下しか置けない・・・)
このことから、Sの列は各列に少なくとも1つ「0」がなければならない。
もしそうでないとすると、5の列で考えると5より大きい数を取っていって6番目が9。これは無
理で、他はよりきつい。Sは9列あるから、「0」が少なくとも9個あることになる。
一方、各行で2個で、5行だから、「0」は全部で10個である。
(n=12のときと違って、1だけ差がある) もちろん、2行目から6行目を考えている。
Mは6以下だから、少なくとも一方のMは、5以下。従って、Mが2つとも0でないとすると上と
同様に考えて、Rの2列のうち少なくとも一方に0がなければならない。
L=1 のとき、Cより大きいのはDよりないから、Cの下またはその下が「0」であるが、さら
にもう1個、この列に「0」がないと、L=1にはなれない。
従って、このとき、Lの列に「0」は少なくとも2個ある。
同様に考えて、K=1、2 のとき、Kの列に「0」が少なくとも2個ある。
3つの条件 「MMはともに0でない」 「Lは1」 「Kは1または2」 を考える。
このうちの2つが成り立てば、「0」は11個以上となって矛盾である。
従って、このうちのせいぜい1つしか成り立たない。即ちこれらの否定が2つ以上成り立つ。
Lの位置には最終的に、「2」が入ることになるから、Lはそれより小さい「0」か「1」しかない。
同様に、Kは、「0」か「1」か「2」しかない。
ということで、上の3つの条件の否定は、「MMの一方は0」 「Lは0」 「Kは0」となる。
このうちの2つ以上が成り立たねばならないが、それは不可能である。
なお、6巡+0手や5巡+数手で不可能なことも容易に示される。(証終)
GAI さんが、n=10、11、12、13 の場合の手順を見出された。
(平成22年6月30日、7月1日付け)
n=10
00123456789A ⇒
1263450789A0 ⇒
237450189A06 ⇒
3487652A0019 ⇒
40987650213A ⇒
51A987643200 →→→→→
00A987654321
n=11
00123456789AB ⇒
1273456089AB0 ⇒
238560719AB04 ⇒
34987602AB015 ⇒
45A987630012B ⇒
56BA987413200 →→→→→→
00BA987654321
n=12
00123456789ABC ⇒
1234657C89AB00 ⇒
234576A090BC18 ⇒
34568702A1C09B ⇒
45A798630201BC ⇒
56CBA987143200 →→→→→→
00CBA987654321
n=13
00123456789ABCD ⇒
1283456709ABCD0 ⇒
2394568A1BCD007 ⇒
34A9670B2CD0158 ⇒
45BA98703D0126C ⇒
56CBA987401230D ⇒
67DCBA985243010 →→→→→→→
00DCBA987654321
(コメント) n=13 のとき、85手で、らすかるさんの結果により、これが最短手数となる。
このことから、これまでの最短手数をまとめると、
| 数字の個数(n) | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 最短手数 | 3 | 5 | 6 | 13 | 21 | 25 | 28 | 41 | 55 | 61 | 66 | 85 |
となる。
FNさん、らすかるさん、GAI さんのご尽力により、このパズルも非常な深化を遂げたが、
ここで、FNさんが、
冒頭の問題(n=5のとき)で、13手が最小である
ことの証明を、当初の問題に即して与えられた。(平成22年7月1日付け)
|
(証明) まず、5は動かないといけないから、5手はかかる。そうすると、3は一度動いてか
らもとに戻らないといけないから、最低8手は必要。
8手以上12手以下の何手かでできると仮定する。
最初と5手目、10手目の直後を書く。ただし、8手や9手でできるときは10手目はないか
ら最終手とする。13手目以降がないから、10手目(or最終手)の段階で、「 5 4 3 」
は正しい位置にきている。
| 最初 |
|
|||||||||||||||||||||
| 5手目 | ||||||||||||||||||||||
| 10手目(または最終手) |
5は最後に動かすから、Cは空である。Aに、1、2、3はこれない。Aに4や5がくると、そ
の下に3はこれない。従って、Aも空である。
Bは、5か空しかないが、空はありえないから、Bは5である。
そうなると、Dは空しかないので、10手以内でできることはありえない。
すなわち、11手か12手の可能性が残る。
わかった所を書きこむと、
| 最初 |
|
||||||||||||||||||||||||||||
| 5手目 | |||||||||||||||||||||||||||||
| 10手目(または最終手) | |||||||||||||||||||||||||||||
| 最終手 |
上表で、I は空でなければならない。そうすると、G、Hの一方は1。従って、E、Fの一方は
空となるが、これはあり得ない。 (証終)
さらに、FNさんは、この問題について、新たな端緒を開かれた。(平成22年7月1日付け)
冒頭の問題の最短手数は13手であるが、最短手数を与える手順は何通りあるか?
ただし、最初に空所2ヶ所を逆に入れたものは同じとみなすことにする。初手は1を空所
に入れるしかないが、左に入れるとしておく。
この問題に対して、らすかるさんが解を示された。(平成22年7月2日付け)
| 数字の個数(n) | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 手順パターン数 | 1 | 1 | 1 | 2 | 21 | 37 | 37 | 4082 |
となる。
らすかるさんの示された結果により、n=5 の場合は手順が2通りあるが、その具体的な
手順を、FNさんが求められた。(平成22年7月2日付け)
| 0012345 ⇒ 1243500 ⇒ 2354010 →→→ 0054321 |
と | 0012345 ⇒ 1243050 ⇒ 2354100 →→→ 0054321 |
(求め方) まず、11手目以降は指定席に置くだけの必然手なので、10手目(2巡目)まで
で考えれば十分。n=5 の場合、
0012345 ⇒
RRXXSST ⇒
RR54SST →→→
0054321
必然的に、Tは2つとも0。Sの列に少なくとも1つ0があるが、そうすると、0の個数は4以
上となり、従って、Sの列には0がちょうど1つ、RやXの列には、0はなしとなる。
左の0の下のRは1との約束なので、上のRRは「 1 2 」、下のRRは「
2 3 」しかない。
2の下のXは3しかない。これまでのところを書くと
0012345 ⇒
12X3SS0 ⇒
2354SS0 →→→
0054321
1の下のXは、4、5、0 しかないが、0はだめで、5もだめだから、4しかない。
残ったSの所は、各行、各列に0が1個だから、「 0 S 」か「 S 0
」しかない。
残った所に残った数字を入れて、上に書いた2つになる。
(コメント) FNさんの説明で、考え方の基本が段々分かってきたような気がします...。
FNさんによれば、最短手数の手順の個数を考えようとしたのは最短手数の手順の存在
の証明をするためにどの程度ありそうかの感じをつかむためだったとのこと。
らすかるさんの証明にあるように、n を4で割った余りによって状況が微妙に変わります。
n=5は、n=4k+1のパターンなので、まずこのパターンから考えてみたいと思う。
(FNさん 平成22年7月2日付け)
このときの最短手数は、2k巡2k+1手である。いきなり一般の場合は難しいので、まず
k=2 即ち、n=9のときを考える。
00123456789
RRXXXSSSSTT
RRXXXSSSSTT
RRXXXSSSSTT
RR9876SSSTT
n=5のときと同様に、0は、SとTで使い切る。従って、S列には、0がちょうど1個ずつで、
R列X列にはない。このことからRRは決まる。また、3の列も決まる。9の列の2つの0も決ま
る。このあたりは、n=4k+1で成り立つ。
00123456789
12XX4SSSST0
23XX5SSSSTT
34XX6SSSSTT
459876SSST0
もちろん、n=9のときに最短手数の手順があることはすでにわかっていて、らすかるさん
によると、4082通りもあるとのこと。
従って、その手順を作るだけでは意味がなく、n=4k+1のときに一般化できるようなもの
を作らないといけない。
上記のFNさんの考察を受けて、HN「攻略法」さんが、具体的な解の手順を示された。
(平成22年7月29日付け)
Nによって、一般に、最少手数 M の計算
・Nが奇数なら、M=(N2+1)/2
・Nが偶数で、N=4k型 なら、M=(N−1)N/2
N=4k+2型 なら、M=N(N+1)/2
手順は、INT(M/N)巡+MOD(M,N)手と簡潔に記述できる。(以下この表記とする)
手順は、次の2つのパターンに大別できる。
■奇数、偶数4k型の場合 ※下記のStep6まで
N= 24 M= 276
xrs t w
ZZXXXXXXXXXXXXYYYYYYYYYYYY
0 0+123456789ABCDEFGHIJKLMNO {} ※ + は0の意、. は未定
24 12E3456789ABCD+FGHIJKLMNO0 {}
48 23FE56789ABCD+1GHIJKLMNO0. {4}
72 34GFE789ABCD+52HIJKLMNO01. {6}
96 45HGFE9ABCD+763IJKLMNO012. {8}
120 56IHGFEBCD+9874JKLMNO0123. {A}
144 67JIHGFED+BA985KLMNO0.234. {1C}
168 78KJIHGFEDCBA960MNO+1.345. {2L}
192 89LKJIHGFEDCBA71NO+32.056. {4M}
216 9AMLKJIHGFEDCB82O+543.107. {6N}
240 ABNMLKJIHGFEDC93+7654.210. {8O}
264 BCONMLKJIHGFEDA4987650321+ {}
+12手
■偶数4k+2型の場合
N= 26 M= 351
rs w
ZZXXXXXXXXXXXXXYYYYYYYYYYYYY
0 0+123456789ABCDEFGHIJKLMNOPQ {}
26 12E3456789ABCD+FGHIJKLMNOPQ0 {}
52 23FE56789ABCD+1GHIJKLMNOPQ0. {4}
78 34GFE789ABCD+52HIJKLMNOPQ01. {6}
104 45HGFE9ABCD+763IJKLMNOPQ012. {8}
130 56IHGFEBCD+9874JKLMNOPQ0123. {A}
156 67JIHGFED+BA985KLMNOPQ01234. {C}
182 78KJIHGFEDCBA960MNOPQ+12345. {L}
208 89LKJIHGFEDCBA7.NOPQ+103456. {2M}
234 9AMLKJIHGFEDCB8.OPQ+3210567. {4N}
260 ABNMLKJIHGFEDC9.PQ+54321078. {6O}
286 BCONMLKJIHGFEDA.Q+765432109. {8P}
312 CDPONMLKJIHGFEB.+9876543210. {AQ}
338 D0QPONMLKJIHGFECBA987654321+ {}
+13手
★パターンの生成(概要)
数字列を、ZZXXXXYYYYに分ける。
Z並びは2個、Y並びはMOD(M,N)個、X並びは(N-(Y並びの個数))個となる。
また、巡回数を j 、X並びの最小値を v=N−j+1 とする。
例 N=9 の場合、Mは41手、Xは4個、Yは5個、j は4、v は6となる。
(Step 1) 巡回列
Z列を、00,12,23,34,45,56,…とする。ただし、4k+2型(N=6,10,14,18,22,…)の場合は、Z並
びの(j)(j+1)部分を(j)(0)に置き換える。
例 N=9 の場合
ZZXXXXYYYYY
0 00123456789
9 12xxxxyyyyy
18 23xxxxyyyyy
27 34xxxxyyyyy
36 45xxxxyyyyy
例 N=10 の場合
ZZXXXXXYYYYY
0 00123456789A
10 12xxxxxyyyyy
20 23xxxxxyyyyy
30 34xxxxxyyyyy
40 45xxxxxyyyyy
50 50xxxxxyyyyy
(Step 2) 降順列
巡を重ねることで、X並びを降順に1つずつ揃えて整列させる。v が対角線に並ぶ。
例 N=9 の場合
ZZXXXXYYYYY
0 00123456789
9 126xxxyyyyy
18 2376xxyyyyy
27 34876xyyyyy
36 459876yyyyy
(Step 3) 2つの0の位置を仮定する。
X並びに、1巡(v−1)列から左下斜めに向かって、先のX並びの降順に重なるまで0を記
入する。
Y並びに、1巡右端列から左下斜めに向かって、(最終行−1)行まで0を記入する。
s並び(s列)を、v列に設ける。その終端(X並びの0が、先のX並びの降順に重なる行)を
0とする。
Y並びに、最終行右端列から左上斜めに向かって、s並びの終端1つ前まで0を記入する。
例 N=9 の場合
rs
ZZXXXXYYYYY
0 00123456789
9 ZZXxxx0syy0
18 ZZXXx0ysy0y
27 ZZXXXxy+0yy ←終端
36 ZZXXXXyyyy+ ※大文字は既に数字が確定されている
(Step 4) r並び(r列)
r並びを、(v−1)列に設ける。0,1,2,3,4,…とする。(Z並びの数字と連続させる)
ただし、4k+2型の場合、最終行でX並びと重なるので上書きしない。
例 N=9 の場合
rs
ZZXXXXYYYYY
0 00123456789
9 ZZXxxx0syy0
18 ZZXXx01sy0y
27 ZZXXXx2+0yy
36 ZZXXXX3yyy+ ※大文字は既に数字が確定されている
(Step 5) 最終行(最終巡回行)
4k型の場合、X並び(r並びの1つ前)が埋まっていないので、(降順列で)充填する。
まず、Y並びを降順列で埋める。ただし、4k+2型以外の場合は、未使用の0を右端から
INT(j/2)の位置に当てはめる → t並び(t列)
s並びは、取り除いた数字が入れる
と補正する。
例 N=9 の場合
rs t
ZZXXXXYYYYY
0 00123456789
9 ZZXxxx0syy0
18 ZZXXx0Rsy0y
27 ZZXXXxR+0yy
36 ZZXXXXR120+ ※大文字は既に数字が確定されている
(Step 6) 昇順列、降順列で埋める
0に向かって(矢印の向きに)昇順列、降順列で埋めていく。
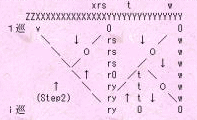
以上の操作で、s並びの下、t並び、w並び(右端列)を除いてすべて埋まる。
例 N=9 の場合
rs tw
ZZXXXXYYYYY
0 00123456789 {}
9 12634507890 {}
18 2376501890y {4}
27 348765200yy {19}
36 45987631200 {}
(Step 7) s並びの下、t並び、w並びを埋める。ほとんど自明である。 完成!!!
ちなみに、奇数(N=4k+1)の場合
N=13
0 0+123456789ABCD
13 12834567+9ABCD0
26 2398567+1ABCD04
39 34A987+52BCD016
52 45BA987630D+12C
65 56CBA98741+230D
78 67DCBA98524301+
+7手
N=17
0 0+123456789ABCDEFGH
17 12A3456789+BCDEFGH0
34 23BA56789+1CDEFGH04
51 34CBA789+52DEFGH016
68 45DCBA9+763EFGH0128
85 56EDCBA98740GH+123F
102 67FEDCBA9851H+2304G
119 78GFEDCBA962+43510H
136 89HGFEDCBA73654021+
+9手
N=21
0 0+123456789ABCDEFGHIJKL
21 12C3456789AB+DEFGHIJKL0
42 23DC56789AB+1EFGHIJKL04
63 34EDC789AB+52FGHIJKL016
84 45FEDC9AB+763GHIJKL0128
105 56GFEDCB+9874HIJKL0123A
126 67HGFEDCBA9850JKL+1234I
147 78IHGFEDCBA961KL+23045J
168 89JIHGFEDCBA72L+435106K
189 9AKJIHGFEDCB83+6547210L
210 ABLKJIHGFEDC9487650321+
+11手
N=25
0 0+123456789ABCDEFGHIJKLMNOP
25 12E3456789ABCD+FGHIJKLMNOP0
50 23FE56789ABCD+1GHIJKLMNOP04
75 34GFE789ABCD+52HIJKLMNOP016
100 45HGFE9ABCD+763IJKLMNOP0128
125 56IHGFEBCD+9874JKLMNOP0123A
150 67JIHGFED+BA985KLMNOP01234C
175 78KJIHGFEDCBA960MNOP+12345L
200 89LKJIHGFEDCBA71NOP+230456M
225 9AMLKJIHGFEDCB82OP+4351067N
250 ABNMLKJIHGFEDC93P+65472108O
275 BCONMLKJIHGFEDA4+876593210P
300 CDPONMLKJIHGFEB5A987604321+
+13手
N=29
0 0+123456789ABCDEFGHIJKLMNOPQRST
29 12G3456789ABCDEF+HIJKLMNOPQRST0
58 23HG56789ABCDEF+1IJKLMNOPQRST04
87 34IHG789ABCDEF+52JKLMNOPQRST016
116 45JIHG9ABCDEF+763KLMNOPQRST0128
145 56KJIHGBCDEF+9874LMNOPQRST0123A
174 67LKJIHGDEF+BA985MNOPQRST01234C
203 78MLKJIHGF+DCBA96NOPQRST012345E
232 89NMLKJIHGFEDCBA70PQRST+123456O
261 9AONMLKJIHGFEDCB81QRST+2304567P
290 ABPONMLKJIHGFEDC92RST+43510678Q
319 BCQPONMLKJIHGFEDA3ST+654721089R
348 CDRQPONMLKJIHGFEB4T+876593210AS
377 DESRQPONMLKJIHGFC5+A9876B43210T
406 EFTSRQPONMLKJIHGD6CBA987054321+
+15手
(コメント) 一つ一つ追って理解したいと思います。攻略法さんに感謝します。
以下、工事中