
下図のように同じ大きさの立方体が8個積まれていて、5頂点 O、A、B、C、D を考える。
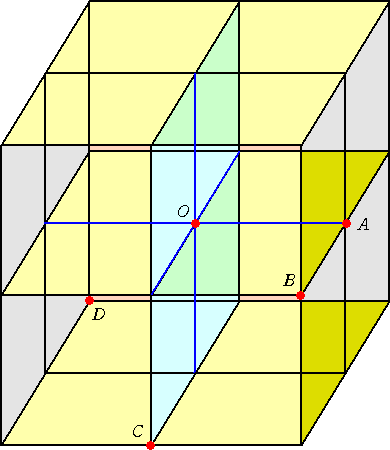
これらの頂点を結ぶ4本の直線 OA、OB、OC、OD の上に1点ずつ 4点を上手くとると、
平行四辺形が作れるという。 どのように4点を選んだらいいのだろうか?
(答) 線分OA、OC、ODの中点をそれぞれ A’、C’、D’ とすると、四角形 A’BC’D’ が
求める平行四辺形となる。
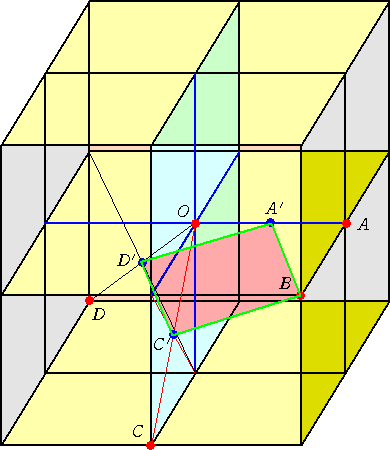
中点連結の定理を意識すれば、それほどの困難さもなく平行四辺形を見つけることはで
きるだろう。
上記の問題では5点を指定しているが、もっと一般的に次の事実が成り立つ。
空間の1点 O を通る4直線で、どの3直線も同一平面上にはないものとする。
このとき、4直線の何れにも点 O 以外の点で交わる平面で、4つの交点が平行四辺
形の頂点になるものが存在する。
この事実を証明する問題が、平成20年度入試 京都大学 理系(理・乙)で出題された。
ベクトルを用いて、上記の問題は次のように機械的に解かれる。
OA=( 1 , 0 , 0 ) 、 OB=( 1 , −1 , 0 ) 、
OC=( 0 , −1 , −1 ) 、 OD=( −1 , 1 , −1 )
とおくと、 OA=2OB−OC+OD が成り立つので、
OA=2OA’ 、 OC=2OC’ 、 OD=2OD’
となるように、点A’、C’、D’ を定めると、 2OA’=2OB−2OC’+2OD’ から
D’A’=C’B が成り立ち、四角形 A’BC’D’ は平行四辺形となる。
京都大学の入試問題も、1次独立な3つのベクトルで、残りのベクトルが線形結合で表さ
れることから同様に示される。解答は読者にまかせよう。