下図のような、３×７のマス目の板がある。
このマス目の全てにオセロの駒（一方が黒、他方が白）を任意に置いていく。このとき、
どのような置き方をしても、次の条件（１）（２）の全てを満たす４つの駒が存在する。
条件 （１） ４つの駒は、全て黒または白である。
（２） ４つの駒を頂点とする図形は長方形である。
これは、本当だろうか？
例えば、次のように置いたとき、確かに長方形が存在するが．．．！
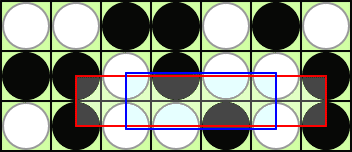
（答） 本当である。
実際に、まず１行目に着目して、白か黒どちらかは４個以上あるはずである。
いま、白の方が４個以上あるものとし、その列に注目する。（下図参照）
次に、その列のうち、２行目に白が２個以上あれば題意は満たされるので、左図のように、その列に黒が
３個以上ある場合を考えればよい。
２行目が黒の列に注目して、３行目に黒が２個以上あれば題意は満たされる。
逆に、白が２個以上あれば、１行目の白と組み合わせると題意は満たされる。
（参考文献： 全米数学オリンピック問題）
（追記） 当ＨＰがいつもお世話になっているらすかるさんから別解を頂いた。
（平成１８年１月４日付け）
上記では、横の並びに注目したが、縦の並びに注目してもよい。
縦に並ぶ３個の組に注目すると、「白が２つ以上」となるパターンは、
の４通りである。「黒が２つ以上」となるパターンも同様に４通りである。
縦列は全部で７列あり、 どの列も「白が２つ以上」または「黒が２つ以上」のいずれかで
ある。このとき、「白が２つ以上」、「黒が２つ以上」のどちらかは必ず７列中に４列以上は
ある。
その中に、縦列が全て同色のものが含まれていれば、必ず長方形が作られる。
その中に、縦列が全て同色のものが含まれていないとする。たとえば、「白が２つ」が４
列以上あるとすると、
のうち少なくとも一つが２個以上あることになり、長方形が作られる。「黒が２つ」が４列以
上ある場合も同様である。