Minimum 9 
4つの「4」を用いて自然数を作る問題は有名であろう。最近、Webを眺めていたら、
4つの「9」を用いて自然数を作るという問題を授業に取り入れている方がおられた。
豊岡市立竹野中学の吉岡久幸さんのHP:「フォー・ナインズ?」
<問題> 9が四個並んでいます。4個の9と適当な演算記号、√などを使って、
0から30までの自然数を考えてみましょう。
(使って良いもの)
1 四則演算 + − × ÷
2 かっこ ( )
3 9を2つ並べて99とする
4 平方根 √
5 小数点 .9
6 指数
7 階乗 9! ・・・・等
吉岡先生のHPに触発されて、次のような問題を考えてみた。
問 題 1、2、3、・・・ という数を、いくつかの演算といくつかの「9」を用いて表せ。
ただし、用いる「9」の個数は最小限に抑えるものとする。
また、用いてもよい演算は次のものとする。
1 四則演算: + − × ÷
2 かっこ : ( )
3 十進数 : 9を並べて、例えば、99、999、・・・ など
4 累乗根 : 平方根√や3乗根、・・・など
5 小数点 : 「.9」は、0.9を表すものと考える
6 累乗 : 99、・・・など
7 階乗 : 9!、・・・など
8 二重階乗: 9!!=9・7・5・3・1=945、・・・
4!!=4・2=8、・・・ など
9 順列の数: nPr 、nHr
10 組合せ : nCr
11 Γ関数 : Γ(n)=(n−1)!
この問題を設定したのは、「2010」という数を何とか数学的に分解したかったからだ。
当初想定した解は、 2010={(√9)!}!×(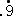 +
+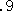 +
+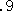 )−(√9)!
)−(√9)!
用いている「9」の個数は、5個。これは、ちょっと不満である。
しかし、二重階乗とΓ関数を用いると、 2010=9!!+9!!+Γ{(√9)!}
と書けることに気がついた。用いている「9」の個数は、3個。これには、満足かな?
さて、2010年正月休みの一服に是非次の表を埋めてみませんか?
ただし、用いる「9」の個数は最小限にしてね...!
| 1 |
= |
|
18 |
= |
|
35 |
= |
|
| 2 |
= |
|
19 |
= |
|
36 |
= |
|
| 3 |
= |
|
20 |
= |
|
37 |
= |
|
| 4 |
= |
|
21 |
= |
|
38 |
= |
|
| 5 |
= |
|
22 |
= |
|
39 |
= |
|
| 6 |
= |
|
23 |
= |
|
40 |
= |
|
| 7 |
= |
|
24 |
= |
|
41 |
= |
|
| 8 |
= |
|
25 |
= |
|
42 |
= |
|
| 9 |
= |
|
26 |
= |
|
43 |
= |
|
| 10 |
= |
|
27 |
= |
|
44 |
= |
|
| 11 |
= |
|
28 |
= |
|
45 |
= |
|
| 12 |
= |
|
29 |
= |
|
46 |
= |
|
| 13 |
= |
|
30 |
= |
|
47 |
= |
|
| 14 |
= |
|
31 |
= |
|
48 |
= |
|
| 15 |
= |
|
32 |
= |
|
49 |
= |
|
| 16 |
= |
|
33 |
= |
|
50 |
= |
|
| 17 |
= |
|
34 |
= |
|
|
|
|
√{( !)!!÷
!)!!÷ }
}
(答) 計算式は一通りには定まらないが、一例をあげておきます。計算式を思いつかれた
方、是非メールでご教示ください。
| 1 |
= |
Γ{Γ( )} )} |
18 |
= |
9+9 |
35 |
= |
9!!÷9÷ |
| 2 |
= |
Γ( ) ) |
19 |
= |
√9H√9+9 |
36 |
= |
9CΓ(√9) |
| 3 |
= |
 |
20 |
= |
Γ( !)÷ !)÷ ! ! |
37 |
= |
√9H(√9)!+9 |
| 4 |
= |
Γ( )+Γ( )+Γ( ) ) |
21 |
= |
9+9+ |
38 |
= |
9CΓ(√9)+Γ( ) ) |
| 5 |
= |
 +Γ( +Γ( ) ) |
22 |
= |
( !)!!÷ !)!!÷ + + ! ! |
39 |
= |
9CΓ(√9)+ |
| 6 |
= |
 ! ! |
23 |
= |
Γ( !)÷ !)÷ !+ !+ |
40 |
= |
Γ( !)÷ !)÷ |
| 7 |
= |
9−Γ( ) ) |
24 |
= |
[√{( !)!!÷ !)!!÷ }]! }]! |
41 |
= |
Γ( !+ !+ )÷ )÷ |
| 8 |
= |
( !)!!÷ !)!!÷ ! ! |
25 |
= |
( !)!!÷ !)!!÷ +9 +9 |
42 |
= |
{9−Γ( )}× )}× ! ! |
| 9 |
= |
9 |
26 |
= |
Γ( !)÷ !)÷ !+ !+ ! ! |
43 |
= |
{Γ( !)+9}÷ !)+9}÷ |
| 10 |
= |
√9H√9 |
27 |
= |
9× |
44 |
= |
( !)!!−Γ( !)!!−Γ( )−Γ( )−Γ( ) ) |
| 11 |
= |
9+Γ( ) ) |
28 |
= |
√9H(√9)! |
45 |
= |
9×( +Γ( +Γ( )) )) |
| 12 |
= |
9+ |
29 |
= |
9× +Γ( +Γ( ) ) |
46 |
= |
√9H9−9 |
| 13 |
= |
√9H√9+ |
30 |
= |
9× + + |
47 |
= |
( !)!!−Γ{Γ( !)!!−Γ{Γ( )} )} |
| 14 |
= |
9+ +Γ( +Γ( ) ) |
31 |
= |
√9H(√9)!+ |
48 |
= |
( !)!! !)!! |
| 15 |
= |
9+ ! ! |
32 |
= |
( !)!!÷ !)!!÷ ×Γ( ×Γ( ) ) |
49 |
= |
( !)!!+Γ{Γ( !)!!+Γ{Γ( )} )} |
| 16 |
= |
( !)!!÷ !)!!÷ |
33 |
= |
9× + + ! ! |
50 |
= |
(√9)!H√9− ! ! |
| 17 |
= |
9+9−Γ{Γ( )} )} |
34 |
= |
9CΓ(√9)−Γ( ) ) |
|
|
|
(*) 「36」はよおすけさんより、それ以外は、ほとんどらすかるさんより頂きました。(H22.1.4)
50までは、「9」が3個以下で書き表すことが出来ました!
