
一辺の長さが1cmの立方体を下図のように積み上げた立体図形を考える。
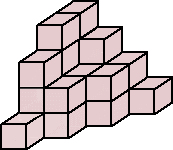
(1) 立体図形の体積を求めよ。
(2) 立体図形の表面積を求めよ。
(答) (1) 24cm3 (2) 64cm2
実際に、(1)は、漏れなく重複なく数えるために、最上段にそれ以下の個数を記入して、
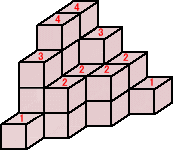
4×2+3×2+2×4+1×2=24(個) より、体積は、 24cm3
(2)は、上下、左右、前後の6方向から見える正方形の面の個数を数える。
この場合、上から見える正方形の面の個数=下から見える正方形の面の個数
右から見える正方形の面の個数=左から見える正方形の面の個数
前から見える正方形の面の個数=後ろから見える正方形の面の個数
であることに注意する。
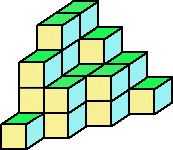
上図で、(緑色):10個 (水色):12個 (黄色):10個 の合計は、32個
よって、求める表面積は、 32×2=64(cm2)