
当HP読者のHN「夏」さんからの出題です。(平成26年3月12日付け)
最近、次の問題を知りました。
(5n+3)/(n5) が自然数となるような自然数 n をすべて求めよ。
nが偶数の時はダメまでは証明できそうなのですが、倍数を一つ一つやって行くのでは解
けそうにありません。この問題は解けるのでしょうか?
教えていただけるとありがたいです(。-_-。)
(答) よおすけさんが考察されました。(平成26年3月12日付け)
n=1 のとき、 51+3=8、15=1 なので、与式=8 となり成り立つ。
n=2 のとき、 52+3=28、25=32 となり、与式=28/32 となり自然数にならない。
n=3 のとき、 53+3=128、35=243 となり、与式=128/243 となり、自然数に
ならない。
これを繰り返しても、同様の結果が続く。よって、条件を満たす自然数nは、1のみ。
(おおざっぱな解答になってしまったことをお詫びします。)
(コメント) グラフ描画ソフトを用いて、y=(5n+3)/(n5) の変動を眺めると面白いですね!
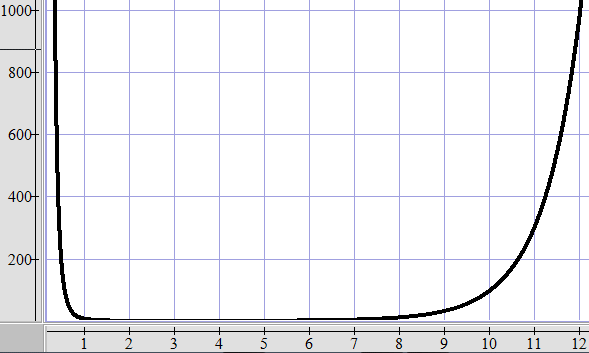
上記のグラフから分かるように、グラフは基本的に増加関数である。よおすけさんの解法
は、小さいnの値を調べて自然数にならないから解はないと判断されているような雰囲気な
のだが、増加関数なので、途中で自然数になる可能性は否定できない。そこら辺の事情を
グラフから求めることは至難の技なので、数式処理で追究するしかないだろう。
ABCDEFさんからのコメントです。(平成26年3月14日付け)
フェルマーの小定理より、奇素数pに対して、2p-1−1はpの倍数です。では、2p-1−1がp2
の倍数になることはあるでしょうか。p<1000の範囲にはありませんでした。これを満たす素
数pはあるのでしょうか?
DD++さんからのコメントです。(平成26年3月14日付け)
ヴィーフェリッヒ素数のことでしょうか。1093、3511、・・・その先は不明。
ABCDEFさんからのコメントです。(平成26年3月14日付け)
ヴィーフェリッヒ素数というのですか。1000まで調べたのですが、もうちょっと調べていたら
みつかったのですね。
3p-1−1 が p2 で割り切れる素数として、p=11は気がついていたのですが、その次が
1006003と書いてあってびっくりしました。このように、めったにないということは、3p-1−1 が
p3で割り切れる素数は存在しないように思いますが、これは証明されているでしょうか。
GAI さんからのコメントです。(平成26年3月14日付け)
少し調べましたら、5p-1−1 がp2で割り切れる素数pは、
20771 、40487 、53471161 、1645333507 、6692367337 、188748146801
7p-1−1 がp2で割り切れる素数pは、 5 、491531
11p-1−1 がp2で割り切れる素数pは、 71
13p-1−1 がp2で割り切れる素数pは、 863 、17475591
17p-1−1 がp2で割り切れる素数pは、 3 、46021 、48947
19p-1−1 がp2で割り切れる素数pは、 3 、7 、13 、43 、137 、63061489
だそうです。
ABCDEFさんからのコメントです。(平成26年3月14日付け)
多分、相当大きな数まで調べてこのような結果になってるのでしょう。ということは非常に
まれな現象なのでしょうが、19以下のすべての素数について、少なくとも1つはあるのが面
白いです。p3で割り切れるのはやはりないのでしょうね。
DD++ さんからのコメントです。(平成26年3月15日付け)
53p-1−1 がp3で割り切れる(p=3)。251p-1−1 がp3で割り切れる(p=5)。
163p-1−1 がp4で割り切れる(p=3)。
簡単な数の冪でないとはいえ、こうもあっさり実例を見つけられるのですから、2や3の冪
の場合に条件を満たす数がないとは簡単には言い切れないように思います。
ABCDEFさんからのコメントです。(平成26年3月15日付け)
その通りですね。書き方が不適切でした。
a≡1、-1 (mod p)であれば、ap-1≡1 (mod p3) になることは十分にありえます。
「a≡1、-1 (mod p)でない場合で」と書かないといけませんでした。それでも反例はあるかも
しれませんが。
フェルマーの小定理より、奇素数pに対して、2p-1−1はpの倍数です。では、2p-1−1がp2
の倍数になることはあるでしょうか。
これは夏さんの冒頭の質問に関連したものです。少し調べてみれば、n=1 以外はなさそう
だとわかります。そこで、それを証明しようとします。
(A) n(≠1)が自然数であるとき、5n+3はn5で割り切れない。
少し強めて、次の形で成立するのではないかと考えました。
(B) pが自然数nの素因数であるとき、5n+3はp5で割り切れない。
ここで、「p5」はもっと小さくできるのではないかと考えました。p=2のときは、「p3」、p=3、5の
ときは「p」でいいと分かります。証明は容易だから省略します。
そこで、p>5のときは、「p2」でいいのではないかと考えました。
(C) p(>5)が自然数nの素因数であるとき、5n+3はp2で割り切れない。
これが成り立たないようなn、pがあれば、n=pkとおいて、 5pk≡−3 (mod p2)
両辺を p-1 乗して、 (5p(p-1)) k≡3p-1 (mod p2) で、φ(p2)=p(p-1) だから、
5p(p-1)≡1 (mod p2) より、 3p-1≡1 (mod p2) となる。
(D) 3p-1≡1 (mod p2) となる素数pは存在しない。
もし、これが言えたら(多少の例外は気にしない。p=11では不成立)、(C)が成り立ち終わり
というつもりだったのですが、(D)は証明不可のようなので、この方針は駄目ということになり
ます。(D)は無理と分かった、(C)は成り立つのではないかと思います。もちろん、p=3、5は当
然成り立つので、「p>5」は、「p>2」で十分ですが、p=3、5は特殊なので、「p>5」としていま
す。
DD++ さんからのコメントです。(平成26年3月15日付け)
では、19p-1−1 がp3で割り切れる(p=7)とか?
ABCDEFさんからのコメントです。(平成26年3月15日付け)
そうですね。調べもしないで、いい加減なことばかり書いてます。1<a<p-1とすればどう
かと思ったのですが、これでも、p=113のとき、68p-1−1 がp3で割り切れるとなりました。
DD++ さんからのコメントです。(平成26年3月15日付け)
その制限での反例は見つける自信がありませんでしたが、やはりありましたか。私も夏さ
んの問題を考えているのですが、これって、そもそも (5n+3)/n が自然数になるものはいく
つあるのでしょうかね。3の倍数、5の倍数、8の倍数、7以上の素数がダメなことはすぐ確認
できます。逆に、自然数になる具体例は、n=1、2、4、14、(さてこの先はあるのでしょうか?)
特に、1以外の奇数解はあるのでしょうか?もし、この先奇数解がなければ、「/n3」の時点
でもう「n=1」しか自然数にならないわけですが...。
ABCDEFさんからのコメントです。(平成26年3月15日付け)
(5n+3)/n が自然数になるものは、n≦100000の範囲で調べたら、
n=1、2、4、14、628、11524、16814
でした。このうち、(5n+3)/n2 が自然数になるのは、「n=1、2」だけです。
DD++ さんからのコメントです。(平成26年3月15日付け)
ありがとうございます。早いですね。感触としてはやはり奇数解は1しかなさげでしょうか。
何が要因でそうなっているのかさっぱり検討がつきませんが...。
攻略法さんからのコメントです。(平成26年3月16日付け)
5n−1や5n+3は、4の倍数ですね。
らすかるさんからのコメントです。(平成26年3月16日付け)
52m+3≡4 (mod 8) なので、偶数はありえないですね。
冒頭の問題について、当HP読者のHN「Y.I.」さんより、「nが素数のとき、解がない」旨、
メールでお知らせ頂いた。(平成26年3月16日付け)
(5n+3)/(n5) について、nが素数の時に解がないことの証明ができました。
1.pを奇素数として、(5p+3)/p は整数にならない。
実際に、11以上の素数pについて、フェルマーの定理より、 5p ≡ 5 (mod p) なので、
5p+3 ≡ 8 (mod p)。このとき、5p+3は、p、すなわち、p5で割り切れることはない。
(一般に、a が b で割り切れないとき、a は、bc で割り切れない。)
p=3,5,7については、計算で確かめると、5p+3は、p5で割り切れない。
2.このことから、(5p+3)/(p5) が自然数となる奇素数pは存在しない。
3.奇素数でない2の場合は、計算によって明らか。
空舟さんからのコメントです。(平成26年3月16日付け)
オンライン整数列大辞典を紐解くと、「A123052」(5n+3がnで割り切れるnの数列)に出
会いますね。
DD++ さんからのコメントです。(平成26年3月16日付け)
この数列に、5の倍数が登場するはずがないと思うのですが、果たしてこの「A123052」は
どこまで信用してよいのやら。
ABCDEFさんからのコメントです。(平成26年3月16日付け)
確かに変ですね。これらが条件を満たすかどうか調べてみたら、3984724まではOKでした。
もちろん3984724以下に他にはないという意味ではありません。172315684を調べようとした
らMaximaさんは黙ってしまいました。
ついでに、ひょっとして3の倍数が含まれてないか調べてみたら、3850302156と11028887367
が3の倍数でした。これらも条件を満たさないのは明らかです。少なくとも4個は正しくないも
のが紛れ込んでいます。
ABCDEFさんからのコメントです。(平成26年3月16日付け)
転記ミスと思いたいけど、それにしては多すぎます。オンライン整数列大辞典というのは誰
かが責任をもってチェックしているのではないのではないのでしょうか。「間違っている」と連
絡すれば訂正されるのでしょう。高速なプログラムが書ける人がおられたらどれが正しくてど
れが間違いか調べていただけたらありがたいと思います。
らすかるさんからのコメントです。(平成26年3月16日付け)
オンライン整数列大辞典は膨大な量ですし、そもそもチェック不可能なデータが多いですか
ら、チェックはしていないと思います。
プログラムは特に高速でなくても、べき乗を分解すれば、基本的に「2乗」と「乗算」と「剰余」
で比較的簡単に求められます。計算結果は以下の通りです。
208268941 まで正しく、3850302156以降はすべて間違いです。
5^2+3≡0 (mod 2) 、5^4+3≡0 (mod 4) 、5^14+3≡0 (mod 14) 、5^628+3≡0 (mod 628)
5^11524+3≡0 (mod 11524) 、5^16814+3≡0 (mod 16814) 、5^188404+3≡0 (mod 188404)
5^441484+3≡0 (mod 441484) 、5^2541014+3≡0 (mod 2541014)
5^3984724+3≡0 (mod 3984724) 、5^172315684+3≡0 (mod 172315684)
5^208268941+3≡0 (mod 208268941) 、5^3850302156+3≡2696690452 (mod 3850302156)
5^6234894811+3≡2278994073 (mod 6234894811)
5^11028887367+3≡8096794217 (mod 11028887367)
5^19300390994+3≡28 (mod 19300390994)
5^40545168298+3≡17855737722 (mod 40545168298)
5^81605925785+3≡3128 (mod 81605925785) 、5^84241984285+3≡3128 (mod 84241984285)
5^114992136598+3≡84539823120 (mod 114992136598)
5^131593374346+3≡75484033896 (mod 131593374346)
5^501743327011+3≡453049088328 (mod 501743327011)
自作電卓ソフトで計算し、「WolframAlpha」で答え合わせしました。それにしても、ひどい間
違いですね。
ABCDEFさんからのコメントです。(平成26年3月16日付け)
ありがとうございます。比較的簡単に求められるのですか。とてもできそうには思えません
でした。
historyによると、3850302156以下はすべてLars Blombergという人によって、2011年11月25
日に書き込まれたもののようです。ひどい人もいたものです。是非正しいデータをオンライン
整数列大辞典に連絡してください。
らすかるさんからのコメントです。(平成26年3月17日付け)
例えば、 5^628 を628で割った余りを求める場合は、
5^628=5^(512+64+32+16+4)=5^512・5^64・5^32・5^16・5^4
と分解して、
5^4=625 、5^8=625^2=390625≡9 (mod 628) 、5^16≡9^2=81 (mod 628)
5^32≡81^2=6561≡281 (mod 628) 、5^64≡281^2=78961≡461 (mod 628)
5^128≡461^2=212521≡257 (mod 628) 、5^256≡257^2=66049≡109 (mod 628)
5^512≡109^2=11881≡577 (mod 628)
なので、 5^628≡577・461・281・81・625=265997・22761・625
≡353・153・625=54009・625≡1・625=625 (mod 628)
よって、 5^628+3≡0 (mod 628)
のように計算すれば、5^nをnで割った余りを求めるのにn^2未満の数しか出てきませんし、
乗算回数もlognに比例する回数ですから、大した計算量ではありません。
とりあえず、「208268941」の次を求めてみたら間違いの原因がわかるかも知れないと思っ
て、適当にプログラムを作ってみたところ、間違いの原因がわかりました。原因は「オーバー
フロー」です。おそらくこの間違った値を投稿した人も、上に書いた方法で求めているものと
思いますが、上記の処理を、int64(符号付き64ビット整数)で行うと、見事に、
3850302156、6234894811、11028887367(以降は確かめていません)
が出てきます。上の計算方法で、n2に近い値が出てきますが、
3850302156^2=14824826692498248336>2^63
ですから、int64の範囲外です。unsigned int64(符号なし64ビット整数)であれば、「3850302156」
は出てきませんので、int64で計算したことは間違いないと思います。今、オーバーフローしな
いようにして、「208268941」の次の数を探しているところです。見つかったら報告します。
※7:57追記 とりあえず、208268941<n≦100億の範囲では、5n+3がnで割り切れるもの
はありませんでした。まだ継続して探していますが、この先にあるのか疑問です。
ABCDEFさんからのコメントです。(平成26年3月17日付け)
原理的には理解できるのですが、実際にプログラムすることはできません。オーバーフロー
してたのですか。それに気づかないで投稿してしまうというのも困ったものです。2年以上も間
違いが指摘されないで残ってしまうのは、もっと困ったことです。「208268941」の次の数が見
つかれば素晴らしいですが、見つからなくても間違ってることの指摘はされた方がいいと思い
ます。間違ったデータが載っているという事態は望ましくありません。
※208268941以下の数は2007年に書き込まれているようです。208268941の次の数が見つ
かれば7年ぶりの新しい数ということになります。
らすかるさんからのコメントです。(平成26年3月17日付け)
プログラムのバグで間違った値が出たとしても、確認できるものはしないといけないですね。
最後の数、2億から120億まで、もう60倍の範囲で見つかっていません。数が大きくなるほど
確率が低くなりますので、これ以上存在しないのかも知れませんね。208268941で何年も止ま
っていたことを考えると、(奇数の完全数のように)あったとしても相当大きな数なのでしょう。
既に「3、5、8の倍数では成り立たない」ということが書かれていますが、「素数の倍数」につ
いてさらに調べてみると、
3、5、11、13、29、31、41、59、71、89、101、・・・の倍数では成り立たず、
7の倍数では、n=7(6m+2)の場合のみ、7で割り切れる
17の倍数では、n=17(16m+5)の場合のみ、7で割り切れる
19の倍数では、n=19(9m+7)の場合のみ、19で割り切れる
23の倍数では、n=23(22m+5)の場合のみ、23で割り切れる
37の倍数では、n=37(36m+16)の場合のみ、37で割り切れる
43の倍数では、n=43(42m+16)の場合のみ、43で割り切れる
・・・・・・・・・・・・・・・・・・・・・・・・・・・・
のようになる。
YI さんからのコメントです。(平成26年3月22日付け)
すっかり忘れられた「(5n+3)/n5」の問題に、これまたすっかり忘れられた手法で挑んで
みました。らすかるさんが、平成26年3月17日付けで、こんな結果を出していました。
(5n+3)/p について、p=3、5、11、13、29、31、41、59、71、89、101、・・・の倍数では成り
立たず、
7の倍数では、n=7(6m+2)の場合のみ、7で割り切れる
17の倍数では、n=17(16m+5)の場合のみ、7で割り切れる
19の倍数では、n=19(9m+7)の場合のみ、19で割り切れる
23の倍数では、n=23(22m+5)の場合のみ、23で割り切れる
37の倍数では、n=37(36m+16)の場合のみ、37で割り切れる
43の倍数では、n=43(42m+16)の場合のみ、43で割り切れる
この結果は疑問な部分がありますが、一般的な構造がつかめることを期待して、この手
法をさらに進めてみました(添付ファイル(圧縮))。
<方法> 5n+3≡0 (mod p) の時、5n≡p-3 (mod p) である(式1)。
(例として、)素数を1つ選び、例えば、7とする。5≡5 (mod 7,以下同様)からスタートし、
52≡4 、53≡6 、54≡2 、55≡3 、56≡1 、57≡5 、(これ以降繰り返し)
また、式1の形が2番目に出てきています。
以上から、5n+3≡0 (mod 7) となるのは、n=6m+2 の時であることがわかります。
この方法を一般化して、別の素数についても検証してみました。
また、式1に一致するものが存在しなければ、「絶対に割り切れない」ことが証明されたこと
になります。今回調べたのは、最初の5000個の素数です。予想に反して、多くの素数が生き
残ってしまいました。この表から、p=n が作れるかどうかですが、難しいような気がします。
私は、除数と指数の関係が現れただけでも満足なのですが...。
らすかるさんからのコメントの続きです。(平成26年3月17日付け)
1000以下の奇素数167個のうち、70個の素数では前者と同様、残りの97個では後者と同様
になります。つまり、
・素因数が多いほど、前者に当たって成り立たない可能性が高くなる
・素因数が大きいほど、後者でも成り立つ確率が小さくなる
ということになりますので、大きい数では条件を満たす確率はかなり小さくなります。
従って、2億から120億まで見つかっていないことを合わせて考えると、これより大きく条件
を満たす数は存在しなくてもおかしくありません。
(確率がいくら小さくても、0でない限り存在する可能性はありますが。)
ABCDEFさんからのコメントです。(平成26年3月17日付け)
そうですか。存在しない可能性もありそうですか。また、「素数の倍数」については私もいく
らか調べたのですが、どちらかというと興味は、
nがpの倍数であるとき、5n+3は、p2で割り切れない
の方にあり、これは私が調べられる程度の値では成り立つし、証明は全くできそうにないし
前に進みません。
また、否定的な結果も大いに意味はあるんですが、印象は肯定的な結果の方があるよう
に思います。(証明できれば別ですが)どの程度の時間がかかるかの見当もつかない素人の
希望ですが、1000億を越えたあたりにでも見つかってくれればいいなと思います。
らすかるさんからのコメントです。(平成26年3月17日付け)
私も「見つかったらいいな」とは思っていますが、予想としては「見つからない」です。現在、
270億を超えたところですから、PCを1週間ぐらい動かしておけば、1000億までは確認できる
と思います。
それから「剰余系におけるべき乗の計算」のプログラムについて、「原理的には理解できる
のですが実際にプログラムすることはできません」とのことでしたが、かなり簡単ですからサン
プルを書いてみます。C言語ならば、
a = 1;
b = 5;
while(n){
if(n & 1)
a = a * b % m;
b = b * b % m;
n >>= 1;
}
※求めるものは5^n (mod m)、aはべき乗計算用変数、bは5^(2^k)計算用変数
(最近の)Visual Basicならば、
A = 1
B = 5
While N > 0
If (N And 1) <> 0 Then
A = A * B Mod M
End If
B = B * B Mod M
N >>= 1
End While
大昔のBASICでビット演算も使わないことにすると、
100 A=1
110 B=5
120 IF N MOD 2<>0 THEN A=(A*B) MOD M
130 B=(B*B) MOD M
140 N=N\2
150 IF N>0 THEN 120
※「\」は整数除算でN\2はINT(N/2)と同じ
# BASICは使い慣れていませんので構文誤りなどあるかも知れません。
らすかるさんが発見されました。(平成26年3月18日付け)
私の予想は外れて、「208268941」の次の値「40874725514」が見つかりました。確かに成り
立つことは、「WolframAlpha」で確認できます。まさか次の値が約200倍のところにあるとは思
いもしませんでしたが、わかっている値を今見直してみると、628→11524, 3984724→172315684
も結構離れていましたね。OEISの数列を修正しようとしたのですが、登録の仕方がわからず、
とりあえず断念しました。
(以前は登録不要だったのですが、知らない間に登録が必要になっていたのですね。)
ABCDEFさんからのコメントです。(平成26年3月18日付け)
私がわかるのは、Excel VBAだけです。それもここ1〜2年はあまり使ってません。らすかる
さんが書かれたのをほんの少し変えてやってみました。
Function MD(N, M)
A = 1
B = 5
While N > 0
If (N And 1) <> 0 Then
A = A * B Mod M
End If
B = B * B Mod M
N = N \ 2
Wend
MD = A
End Function
Sub Test()
N = 100000
For I = 1 To N
X = I
Y = I
Z = MD(X, Y)
If (Z + 3) Mod I = 0 Then
R = R + 1
Cells(R, 1).Value = I
End If
Next
End Sub
以前にやったn≦100000で、5n+3がnで割り切れるnを探すものです。前のは「5をかけて
nで割った余りを求めて」をn回繰り返すというひどいものでした。11524と16814が出るまでに
何分かはかかったと思います。上ので動かすと瞬時でした。演算回数n回とlog2n回程度の
違いですから全然違って当たり前ですが。
ところが、B=46359で、B = B * B Mod Mの行でオーバーフローになってしまいました。調べ
てみると、VBAのLong型は、最大 2,147,483,647(=231-1)で、463592は、これを越えていまし
た。Long型より大きい数を扱える型はないかと調べると、Currency,Double,Variantあたりが
可能性がありそうでしたが、どれで宣言しても結果は同じでした。
Excel自身はもっと大きい数も扱えるので、まさかこの程度でオーバーフローするとは思っ
ていませんでした。Long型は4バイトと書いてあります。それなら、263-1までは扱えていいは
ずだと思うのですが、何故か2バイトまでしか扱えないとは。VBのLong型は263-1までと書い
てありました。
このような計算をするには、Excel VBAは駄目なようです。少なくともVBでないといけないよ
うです。Cの方がいいのでしょうけど。昔はVBを使ったことはあります。
(VB 6.0からVisual Studio.NETのころ)
今使ってるコンピュータにはVBはinstallしてません。VB(あるいはVC)をやるかやめておくか
思案のしどころです。人生の残り時間との相談が必要です。
らすかるさん、見つかりましたか。すばらしい!。是非OEISに登録して数列の修正をしてく
ださい。
らすかるさんからのコメントです。(平成26年3月18日付け)
登録がうまくいかなかったので、Sloaneさんに直接メールを出したら、「A123052」はすぐに
修正されました。私のページも作成されました。
(しかし、メールを出した直後に登録がうまくいくとは…orz)
ところで、多分、Modは整数型で計算するようになっているのですね。Double型にして、
B = B * B
B = B - Int(B / M) * M
に直せば、多分動くと思います。
ABCDEFさんからのコメントです。(平成26年3月18日付け)
確かに修正されていますね。すばらしい!なるほど、Modを使うと自動的にLong型にして
しまうということですね。できました。
Function MD(N, M)
Dim B As Double
A = 1
B = 5
While N > 0
If (N And 1) <> 0 Then
A = A * B - Int(A * B / M) * M
End If
B = B * B - Int(B * B / M) * M
N = N \ 2
Wend
MD = A
End Function
Sub Test()
T1 = Timer
N = 10000000
For I = 1 To N
X = I
Y = I
Z = MD(X, Y)
If Z + 3 - Int((Z + 3) / I) * I = 0 Then
R = R + 1
Cells(R, 1).Value = I
Cells(R, 2).Value = Timer - T1
End If
Next
Cells(R + 1, 2).Value = Timer - T1
End Sub
N=100000だと、1秒かかりませんでした。N=1000000にしても、10秒かかりませんでした。
N=10000000にして、100秒少しでした。初めのプログラムだと、N=100000で20分以上はかか
っていました。Excel VBAで、3984724まで2分かからずに出せるとは!やはり頭は使わない
と駄目だということですね。(私は全く頭を使わなかったけど)その次は桁が2つ上がるからさ
すがに無理でしょう。
追記 B = B * B - Int(B * B / M) * M は、
B = B * B
B = B - Int(B / M) * M
とすべきでした。そのように書かれていたのに。
A = A * B - Int(A * B / M) * M
If Z + 3 - Int((Z + 3) / I) * I = 0 Then
についても同様にすべきでした。
らすかるさんからのコメントです。(平成26年3月18日付け)
時間的な問題だけでなく、桁数的にも多分無理でしょうね。Doubleはおそらく精度16桁程度
で172315684^2>10^16ですから、桁落ちして正しくない結果になると思います。
ちなみに、こちらの環境で(C言語ですが)、3984724までは約1.3秒ぐらいでした。(そういう
速さでないと400億は無理です)7年前のPCですから、最近のPCならさらに速いと思います。
ABCDEFさんからのコメントです。(平成26年3月18日付け)
時間よりもまず精度が問題でしょうね。正確なことを調べないで使ってるので大概の場合は
かなり小さめのところでやめてしまいます。私のPCは5〜6年前のものです。3984724までは
40秒ほどでした。VBAでCの30倍ほどの遅さというのはBasicもなかなか健闘しているというこ
とかもしれません。
DD++さんからのコメントです。(平成26年3月18日付け)
おお、見つかったのですね。すばらしい。「208268941」までが正しかった確認がとれたのも
大きな成果ですね。というわけで、多分皆さん既にやっていらっしゃるでしょうが、
4 = 2^2
14 = 2 * 7
628 = 2^2 * 157
11524 = 2^2 * 43 * 67
16814 = 2 * 7 * 1201
188404 = 2^2 * 19 * 37 * 67
441484 = 2^2 * 19 * 37 * 157
2541014 = 2 * 7 * 181501
3984724 = 2^2 * 43 * 23167
172315684 = 2^2 * 883 * 48787
208268941 = 353 * 589997
40874725514 = 2 * 7 * 8779 * 332569
ふむ。パッと見てわかるような共通点はなさそうですね。やたら末尾4が多いのは気になり
ますが、2つ例外がありますし。ABCDEFさんの方針のほうがゴールまでは近いのかな……?
らすかるさんが発見されました。(平成26年3月23日付け)
15番目が見つかりました。「280454588548」(約2800億;14番目の約7倍)でした。まだ継続
探索中ですので、OEISには後で追加します。当初は1000億までになかったらやめようと思っ
ていましたが、408億の値が見つかったことで、もっと先まで探したくなりました。今は他のPC
も導入して分散探索しています。今日の昼頃には4000億までの探索が終わります。5月には
もっと環境が良くなりますので、10兆ぐらいまで探索できるかも知れません。
YI さんからのコメントです。(平成26年3月23日付け)
なんと、また見つかりましたか。この数列、どこまで続くのでしょう。ところで、
280454588548 = 2^2・997・70324621
と、数が大きくなるほど、大きい素数を含んでいなければならないのでしょうか。
ABCDEFさんからのコメントです。(平成26年3月23日付け)
15番目が見つかりましたか。すごいですね。
「5n+3がnで割り切れる」の5nはそのままで「+3」の部分を変えればどうなるか、OEISで
調べてみました。
5n+1、5n−1はたくさんある。5n+2は、12番目が「915535274009」 (→「A123062」)
5n−2は、7番目が「2670733724929」 (→「A124246」)
5n+3は、15番目が「280454588548」 (→「A123052」) ※上述
5n−3は、18番目が「55606837682」 (→「A123061」)
5n+4は、 7番目が「26675718567」 (→「A123047」)
5n−4は、 5番目が「2353957351049」 (→「A125949」)
5n+5、5n−5はたくさんある。5n+6、5n−6等は見つけられませんでした。
GAI さんからのコメントです。(平成26年3月23日付け)
さらに、「5」の部分を他の数にした場合について、
3n+1≡0 (mod n) (→「A015949」)
3n+2≡0 (mod n) (→「A015973」)
4n+1≡0 (mod n) (→「A015950」)
5n+1≡0 (mod n) (→「A015951」)
6n+1≡0 (mod n) (→「A015953」)
7n+1≡0 (mod n) (→「A015954」)
8n+1≡0 (mod n) (→「A015955」)
9n+1≡0 (mod n) (→「A015957」)
10n+1≡0 (mod n) (→「A015958」)
11n+1≡0 (mod n) (→「A015960」)
12n+1≡0 (mod n) (→「A015961」)
13n+1≡0 (mod n) (→「A015963」)
14n+1≡0 (mod n) (→「A015965」)
15n+1≡0 (mod n) (→「A015968」)
16n+1≡0 (mod n) (→「A015969」)
と調べ尽くしているものですね。らすかるさんを真似して、当てずっぽうで2兆台を調べてい
ましたが、無茶苦茶時間がかかり途中で諦めました。
16番が見つかった旨、らすかるさんより報告があった。(平成26年3月24日付け)
もうすぐ5000億までの探索が終わりますが、5000億到達前に16番目が見つかりました。
「489850370956」でした。初めての末尾「6」です。立て続けに見つかると、いくらでも見つか
るような気がしてしまいますが、今までに見つかっている数から考えると、ここから10兆まで
一つも見つからない可能性も結構ありますね。
YI さんからのコメントです。(平成26年3月27日付け)
「489850370956」は、「2^2*43*373*883*8647」ですね。素因数の多さでも小ささでも初で
しょう。
5n+3が43で割り切れるのは、nが、42x+16の形のとき。
373で割り切れるのは、nが、372x+172の形のとき。
883で割り切れるのは、nが、126x+100の形のとき。
8647で割り切れるのは、nが8646x+1156の形のとき。
これだけの条件を同時にパスするとは、見事な数が見つかったものです。
17番が見つかった旨、らすかるさんより報告があった。(平成26年4月4日付け)
17番目は、1235856817732 (約1兆2千億)でした。