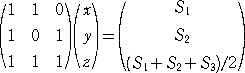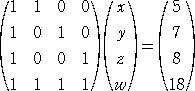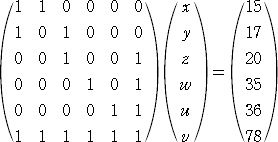２数の和 　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

　当ＨＰがいつもお世話になっているＨＮ「ＦＮ」さんからの出題です。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（平成２３年８月１８日付け）

（１）　５個の数がある。そのうちの２個を取って和をつくると、１０通りの和ができる。
　　　(１０通りの中に同じものがある可能性はある)

　　１０通りの和が、次の通りであったとき、５個の数を求めよ。

　　　　７、１０、１１、１１、１２、１４、１５、１５、１８、１９

（２）　４個の数がある。そのうちの２個を取って和をつくると、６通りの和ができる。
　　　(６通りの中に同じものがある可能性はある)

　　６通りの和が、次の通りであったとき、４個の数を求めよ。

　　　　５、７、８、１０、１１、１３

（０）　３個の数がある。そのうちの２個を取って和をつくると、３通りの和ができる。
　　　(３通りの中に同じものがある可能性はある)

　　３通りの和が、次の通りであったとき、３個の数を求めよ。

　　　　ａ、ｂ、ｃ

　（１）（２）はパズルです。考えてみてください。（０）は（１）（２）との比較のためのもので、ご
く易しい数学です。





























（答え）（０）は３元１次連立方程式です。

　　３数を、ｘ 、ｙ 、ｚ　とおくと、題意より、　ｘ＋ｙ＝ａ　、ｙ＋ｚ＝ｂ　、ｚ＋ｘ＝ｃ

　これより、　ｘ＝（ａ−ｂ＋ｃ）/２　、ｙ＝（ａ＋ｂ−ｃ）/２　、ｚ＝（−ａ＋ｂ＋ｃ）/２

（２）　４個の数を、ｘ 、ｙ 、ｚ 、ｗ　とおくと、２数の和は

　　　ｘ＋ｙ　、ｙ＋ｚ　、ｚ＋ｗ　、ｗ＋ｘ　、ｘ＋ｚ　、ｙ＋ｗ

　　３（ｘ＋ｙ＋ｚ＋ｗ）＝５＋７＋８＋１０＋１１＋１３＝５４　より、　ｘ＋ｙ＋ｚ＋ｗ＝１８

　　このとき、

（イ）　ｘ＋ｙ＝５　、ｚ＋ｗ＝１３　、ｙ＋ｚ＝８　、ｗ＋ｘ＝１０　、ｘ＋ｚ＝１１　、ｙ＋ｗ＝７

（ロ）　ｘ＋ｙ＝５　、ｚ＋ｗ＝１３　、ｙ＋ｚ＝８　、ｗ＋ｘ＝１０　、ｘ＋ｚ＝７　、ｙ＋ｗ＝１１

（ハ）　ｘ＋ｙ＝５　、ｚ＋ｗ＝１３　、ｙ＋ｚ＝１０　、ｗ＋ｘ＝８　、ｘ＋ｚ＝１１　、ｙ＋ｗ＝７

（ニ）　ｘ＋ｙ＝５　、ｚ＋ｗ＝１３　、ｙ＋ｚ＝１０　、ｗ＋ｘ＝８　、ｘ＋ｚ＝７　、ｙ＋ｗ＝１１

（ホ）　ｘ＋ｙ＝１３　、ｚ＋ｗ＝５　、ｙ＋ｚ＝８　、ｗ＋ｘ＝１０　、ｘ＋ｚ＝１１　、ｙ＋ｗ＝７

（ヘ）　ｘ＋ｙ＝１３　、ｚ＋ｗ＝５　、ｙ＋ｚ＝８　、ｗ＋ｘ＝１０　、ｘ＋ｚ＝７　、ｙ＋ｗ＝１１

（ト）　ｘ＋ｙ＝１３　、ｚ＋ｗ＝５　、ｙ＋ｚ＝１０　、ｗ＋ｘ＝８　、ｘ＋ｚ＝１１　、ｙ＋ｗ＝７

（チ）　ｘ＋ｙ＝１３　、ｚ＋ｗ＝５　、ｙ＋ｚ＝１０　、ｗ＋ｘ＝８　、ｘ＋ｚ＝７　、ｙ＋ｗ＝１１

　（イ）について、　ｗ＝１３−ｚ＝１０−ｘ＝７−ｙ　より、

　　　ｘ−ｙ＝３　、ｘ＋ｙ＝５　を解いて、　ｘ＝４　、ｙ＝１　、ｚ＝７　、ｗ＝６

　（ロ）について、　ｗ＝１３−ｚ＝１０−ｘ＝１１−ｙ　より、

　　　ｘ−ｙ＝−１　、ｘ＋ｙ＝５　を解いて、　ｘ＝２　、ｙ＝３　、ｚ＝５　、ｗ＝８

　（ハ）について、　ｗ＝１３−ｚ＝８−ｘ＝７−ｙ　より、

　　　ｘ−ｙ＝１　、ｘ＋ｙ＝５　を解いて、　ｘ＝３　、ｙ＝２　、ｚ＝８　、ｗ＝５

　（ニ）について、　ｗ＝１３−ｚ＝８−ｘ＝１１−ｙ　より、

　　　ｘ−ｙ＝−３　、ｘ＋ｙ＝５　を解いて、　ｘ＝１　、ｙ＝４　、ｚ＝６　、ｗ＝７

　（ホ）について、　ｗ＝５−ｚ＝１０−ｘ＝７−ｙ　より、

　　　ｘ−ｙ＝３　、ｘ＋ｙ＝１３　を解いて、　ｘ＝８　、ｙ＝５　、ｚ＝３　、ｗ＝２

　（ヘ）について、　ｗ＝５−ｚ＝１０−ｘ＝１１−ｙ　より、

　　　ｘ−ｙ＝−１　、ｘ＋ｙ＝１３　を解いて、　ｘ＝６　、ｙ＝７　、ｚ＝１　、ｗ＝４

　（ト）について、　ｗ＝５−ｚ＝８−ｘ＝７−ｙ　より、

　　　ｘ−ｙ＝１　、ｘ＋ｙ＝１３　を解いて、　ｘ＝７　、ｙ＝６　、ｚ＝４　、ｗ＝１

　（チ）について、　ｗ＝５−ｚ＝８−ｘ＝１１−ｙ　より、

　　　ｘ−ｙ＝−３　、ｘ＋ｙ＝１３　を解いて、　ｘ＝５　、ｙ＝８　、ｚ＝２　、ｗ＝３

　以上から、求める４数は、次の２組存在する。

　　　　　　（１，４，６，７）　、（２，３，５，８）

　多分、（１）も同様にできるのだろう。

　求める５数は、　（３，４，７，８，１１）　の１組のみ存在する。


　当ＨＰがいつもお世話になっているＨＮ「攻略法」さんが、（１）（２）の問題を考察された。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（平成２３年８月１９日付け）

　（２）について、４個の数を　ｘ 、ｙ 、ｚ 、ｗ　とする。題意より

　ｘ + ｙ = 5　←式1　、ｘ + ｚ = 7　←式2　、ｘ + ｗ = 8　←式3

　ｙ + ｚ = 10　←式4　、ｙ + ｗ = 11　←式5　、ｚ + ｗ = 13　←式6

式1+式2+式3+式4+式5+式6　より、

　3(ｘ + ｙ + ｚ + ｗ) = 5 + 7 + 8 + 10 + 11 + 13 = 54　　∴　ｘ + ｙ + ｚ + ｗ = 18

式1+式2+式3より、2ｘ + (ｘ + ｙ + ｚ + ｗ) = 5 + 7 + 8 = 20　なので、2ｘ + 18 = 20　より、ｘ = 1

これを、式1、式2、式3に戻して、ｙ = 4、ｚ = 6、ｗ = 7

これらは、式4、式5、式6 を満たすので解となる。

　ここで、ｘ≦ｙ≦ｚ≦ｗ　とすると、各式の右辺（和）は、式1≦式2≦式3、式4≦式5　となる。

また、ｗ を基準に考えると、式3≦式5≦式6 となるので、式3は、

　　最小値、2番目に小さい、2番目に大きい、最大値

を除いたものを考えればよい。これにより、式3は、8、10 が候補となる。

式3が 8 の場合は検証済みなので、式3が 10 の場合を検証すればよい。すなわち、

　ｘ + ｙ = 5　←式1　、ｘ + ｚ = 7　←式2　、ｘ + ｗ = 10　←式3

　ｙ + ｚ = 8　←式4　、ｙ + ｗ = 11　←式5　、ｚ + ｗ = 13　←式6

式1+式2+式3+式4+式5+式6　より、

　3(ｘ + ｙ + ｚ + ｗ) = 5 + 7 + 8 + 10 + 11 + 13 = 54　　∴　ｘ + ｙ + ｚ + ｗ = 18

式1+式2+式3より、2ｘ + (ｘ + ｙ + ｚ + ｗ) = 5 + 7 + 10 = 22　なので、2ｘ + 18 = 22　より、ｘ = 2

これを、式1、式2、式3に戻して、ｙ = 3、ｚ = 5、ｗ = 8

これらは、式4、式5、式6 を満たすので解となる。

　（１）について、５個の数を　ｘ 、ｙ 、ｚ 、ｗ、ｕ　とする。題意より

　ｘ + ｙ = 7 　←式1　、ｘ + ｚ = 10　←式2　、ｘ + ｗ = 11　←式3　、ｘ + ｕ = 14　←式4

  ｙ + ｚ = 11　←式5　、 ｙ + ｗ = 12　←式6　、 ｙ + ｕ = 15　←式7

  ｚ + ｗ = 15　←式8　、ｚ + ｕ = 18　←式9　、 ｗ + ｕ = 19　←式10

式1+式2+式3+式4+式5+式6+式7+式8+式9+式10　より、

　4(ｘ + ｙ + ｚ + ｗ + ｕ) = 7 + 10 + 11 + 14 + 11 + 12 + 15 + 15 + 18 + 19 = 132

　よって、　ｘ + ｙ + ｚ + ｗ + ｕ = 33

式1+式2+式3+式4　より、　3ｘ + (ｘ + ｙ + ｚ + ｗ + ｕ) = 7 + 10 + 11 + 14 = 42

この2式より、 3ｘ + 33 = 42　なので、　ｘ = 3

これを、式1、式2、式3、式4に戻して、　ｙ = 4、ｚ = 7、ｗ = 8、ｕ = 11

これらは、式5、式6、式7、式8、式9、式10 を満たすので解となる。

※「これらは、式5、式6、式7、式8、式9、式10 を満たすので解となる。」としているが、「求
　めた ｘ 、ｙ 、ｚ 、ｗ、ｕ から和を求めて、題意のものが生成されることを確認する」とすれ
　ば、式5〜式10の「和の並び」は気にしなくて良い。

　ここで、ｘ≦ｙ≦ｚ≦ｗ≦ｕ　とすると、各式の右辺（和）は、

　　　式1≦式2≦式3≦式4　、式5≦式6≦式7　、式8≦式9

となる。また、ｕ を基準に考えると、式4≦式7≦式9≦式10 となるので、式3、式4は、

　　最小値、2番目に小さい、3番目に大きい、2番目に大きい、最大値

を除いたものを考えればよい。

これにより、式3、式4は、11、11、12、14、15の中から2つを選んだものになる。

　並び　(式1，式2，式3，式4) は、

　　(7，10，11，11)　、(7，10，11，12)　、(7，10，11，14)　、(7，10，11，15)

　　(7，10，12，14)　、(7，10，12，15)　、(7，10，14，15)

で検証すればよい。

(式1，式2，式3，式4)＝(7，10，11，11)　のとき、

　ｘ + ｙ = 7 　←式1　、ｘ + ｚ = 10　←式2　、ｘ + ｗ = 11　←式3　、ｘ + ｕ = 11　←式4

式1+式2+式3+式4　より、　3ｘ + 33 = 7 + 10 + 11 + 11 = 39　なので、　ｘ = 2

これを、式1、式2、式3、式4に戻して、　ｙ = 5、ｚ = 8、ｗ = 9、ｕ = 9

これらは、式5、式6、式7、式8、式9、式10 を満たさないので解でない。

(式1，式2，式3，式4)＝(7，10，11，12)　のとき、

　ｘ + ｙ = 7 　←式1　、ｘ + ｚ = 10　←式2　、ｘ + ｗ = 11　←式3　、ｘ + ｕ = 12　←式4

式1+式2+式3+式4　より、　3ｘ + 33 = 7 + 10 + 11 + 12 = 40　なので、　ｘ = 7/3

これを、式1、式2、式3、式4に戻して、　ｙ = 14/3、ｚ = 23/3、ｗ = 26/3、ｕ = 29/3

これらは、式5、式6、式7、式8、式9、式10 を満たさないので解でない。

(式1，式2，式3，式4)＝(7，10，11，15)　のとき、

　ｘ + ｙ = 7 　←式1　、ｘ + ｚ = 10　←式2　、ｘ + ｗ = 11　←式3　、ｘ + ｕ = 15　←式4

式1+式2+式3+式4　より、　3ｘ + 33 = 7 + 10 + 11 + 15 = 43　なので、　ｘ = 10/3

これを、式1、式2、式3、式4に戻して、　ｙ = 11/3、ｚ = 20/3、ｗ = 23/3、ｕ = 35/3

これらは、式5、式6、式7、式8、式9、式10 を満たさないので解でない。

(式1，式2，式3，式4)＝(7，10，12，14)　のとき、

　ｘ + ｙ = 7 　←式1　、ｘ + ｚ = 10　←式2　、ｘ + ｗ = 12　←式3　、ｘ + ｕ = 14　←式4

式1+式2+式3+式4　より、　3ｘ + 33 = 7 + 10 + 12 + 14 = 43　なので、　ｘ = 10/3

これを、式1、式2、式3、式4に戻して、　ｙ = 11/3、ｚ = 20/3、ｗ = 26/3、ｕ = 32/3

これらは、式5、式6、式7、式8、式9、式10 を満たさないので解でない。

(式1，式2，式3，式4)＝(7，10，12，15)　のとき、

　ｘ + ｙ = 7 　←式1　、ｘ + ｚ = 10　←式2　、ｘ + ｗ = 12　←式3　、ｘ + ｕ = 15　←式4

式1+式2+式3+式4　より、　3ｘ + 33 = 7 + 10 + 12 + 15 = 44　なので、　ｘ = 11/3

これを、式1、式2、式3、式4に戻して、　ｙ = 10/3、ｚ = 19/3、ｗ = 25/3、ｕ = 34/3

これらは、式5、式6、式7、式8、式9、式10 を満たさないので解でない。

(式1，式2，式3，式4)＝(7，10，14，15)　のとき、

　ｘ + ｙ = 7 　←式1　、ｘ + ｚ = 10　←式2　、ｘ + ｗ = 14　←式3　、ｘ + ｕ = 15　←式4

式1+式2+式3+式4　より、　3ｘ + 33 = 7 + 10 + 14 + 15 = 46　なので、　ｘ = 13/3

これを、式1、式2、式3、式4に戻して、　ｙ = 8/3、ｚ = 17/3、ｗ = 29/3、ｕ = 32/3

これらは、式5、式6、式7、式8、式9、式10 を満たさないので解でない。

以上から、求める解は、　（３，４，７，８，１１）　のみ。


　ＦＮさんからのコメントです。（平成２３年８月２０日付け）

　正解です。

(1)は、下記の4式と10式すべての和から出ますね。

　ｘ + ｙ = 7 　←式1　、ｘ + ｚ = 10　←式2　、ｚ + ｕ = 18　←式9　、ｗ + ｕ = 19　←式10

　もともと５個の数から作ったものなので、式は１０個あっても自由度は５です。上記の４式

と、　ｘ + ｙ + ｚ + ｗ + ｕ = 33　で確定します。もちろん解が残りの式を満たすことの確認は

必要ですが．．．。

(2)は、ｘ + ｗ と ｙ + ｚ の大小が確定しないことから解が２つでます。こちらの方が難しいか

なと思って、(2)にしました。

　そこで、新たな問題です。

（３）　６個の数がある。そのうちの２個を取って和をつくると、１５通りの和ができる。
　　　(１５通りの中に同じものがある可能性はある)

　　１５通りの和が、次の通りであったとき、６個の数を求めよ。

　　　　１５、１７、２０、２１、２２、２５、２５、２６、２７、２８、３０、３１、３２、３５、３６

　これは私は解けてません。もちろん、答えは知っています。自分で適当に６個の数を決め
て、２個ずつの和を書いたのですから。論理的に６個の数を復元することができてないとい
うことです。５個の場合と同様に、５個の式は出ます。もう１個ないといけません。それが何
なのかがわかりません。


　攻略法さんからの続報です。（平成２３年８月２１日付け）

（０）について、連立方程式 Ａｘ＝ｂ　より、　ｘ＝Ａ^-1ｂ　として求める。

　逆行列をもつ行列 Ａ の候補について

個数が、３の場合　ｘ≦ｙ≦ｚ　とする。和を表すものは、₃Ｃ₂＝３　通り

　　ｘ＋ｙ＝Ｓ₁　、ｘ＋ｚ＝Ｓ₂　、ｙ＋ｚ＝Ｓ₃

　上記の式の和から、　ｘ＋ｙ＋ｚ＝（ΣＳ_ｋ）/（３−１）　と、方程式が得られる。

係数を抜き出して行ベクトルで表すと、

　　　

　この４個の方程式から、３つを選んだ連立方程式を考える。連立方程式を解くために、逆
行列をもつ3行3列の行列が必要になる。

　実際に、その組み合わせは、₄Ｃ₃＝４　通りの中で、

が該当する。（括弧は省略、要素の分離にカンマを使う）

　同様に、個数が、４の場合

　このように逆行列をもつ行列Aの候補はいくつかある。

　実際の問題の数値を適用して、「数」の個数 ３、４、５、・・・を見通して選んだ一つの例

個数が、３の場合

←最小値 　←2番目に小さい 　← 和

個数が、４の場合

←最小値 　←2番目に小さい    8 または 10 　←和

　これを解いて、他の式を満たすことを確認して、

　　　　（ｘ，ｙ，ｚ，ｗ）＝（１，４，６，７）　、（２，３，５，８）

個数が、５の場合

←最小値 　←2番目に小さい 　←2番目に大きい 　←最大値 　←和

　これを解いて、　（ｘ，ｙ，ｚ，ｗ，ｕ）＝（３，４，７，８，１１）

個数が、６の場合

←最小値 　←2番目に小さい 　20，21，22，25，26，27，28，30，31，32 　←2番目に大きい 　←最大値 　←和

　これを解いて、　（ｘ，ｙ，ｚ，ｗ，ｕ，ｖ）＝（５，１０，１２，１５，１６，２０）


　ＦＮさんからのコメントです。（平成２３年８月２１日付け）

　個数が、６の場合で、ｚ は、３番目か４番目に大きいから、３１か３２しか可能性はないと
思います。そして、どちらからも解が出ますが、一方は適し、他方は適さないことをチェック
する必要があります。やむをえないのかもしれませんが．．．。

　もともとの問題は、次のようなものです。

ｎ個の数からなる集合をＡとする。Ａから２個を取って作った和の全体をＳ（Ａ）とする。
(Ｓ（Ａ）は同じ数を含む可能性があるから集合とは言えない)

　Ａ≠Ｂ　かつ　Ｓ（Ａ）＝Ｓ（Ｂ）　となることがありうるか。

　ｎ＝２　のときはこれはいくらでもあります。

例えば、Ａ＝{0，3} 、 Ｂ＝{1，2}　とするとき、　Ｓ（Ａ）＝Ｓ（Ｂ）＝{3}

　ｎ＝４　のときも、(２)よりありえます。

　Ａ＝{1，4，6，7} 、 Ｂ＝{2，3，5，8}　とするとき、　Ｓ（Ａ）＝Ｓ（Ｂ）＝{5，7，8，10，11，13}

　ｎ＝３　のとき、ありえないことは(０)からわかります。

　ｎ＝５　のときありえないことは、(１)と同様に確認できます。

　ｎ＝６　のときありえないことも、(３)と同様なのでなんとかなりそうですが、(３)がすっきり解

けたとも言えないので、これを問題にします。

　ｎ＝８　のときは、ｎ＝２、４　と同じ状況になります。

(３Ａ)　ｎ＝６　のとき、A≠B　かつ　S(A)=S(B)　はありえないことを証明せよ。

(４)　ｎ＝８　のとき、A≠B　かつ　S(A)=S(B)　をみたすA、Bを作れ。


　(３Ａ)は私はできてません。(４)は、答は知っています。解はたくさんあります。
(なお、「ｎ個の数」の数は整数、非負整数、自然数とかにしてもかまいません)

　(４)はともかく1個作ればいいので、数学というよりパズルに近いです。ｎ＝２、４　のときの
解を参考にしてつくればいいのですが、そのために、ｎ＝４のときの解をそれぞれから1引い
た形に変えておきます。

　　A＝{0，3，5，6}、Ｂ＝{1，2，4，7} のとき、S(A)＝S(B)＝{3，5，6，8，9，11}


　ＦＮさんからの続報です。（平成２３年８月２８日付け）

(４)　ｎ＝８　のとき、A≠B　かつ　S(A)=S(B)　をみたすA、Bを作れ。

について、例えば、次が解になります。

　　A＝{0，3，5，6，9，10，12，15}　、Ｂ＝{1，2，4，7，8，11，12，14}

　このとき、S(A)=S(B) を確認するのは面倒ですが、作り方からすれば容易にわかります。

　ｎ＝４ のときの A、B を元にして、次のように作りました。

　　A＝{0，3，5，6}、Ｂ＝{1，2，4，7} に対して、

　　　　Ａ’＝A∪(B+8)＝{0，3，5，6，9，10，12，15}

　　　　Ｂ’＝B∪(A+8)＝{1，2，4，7，8，11，12，14}

　このとき、

　　　Ａから異なる2つを取った和とＢから異なる２つを取った和は同じ

　　　B+8 から異なる２つを取った和と A+8 から異なる２つを取った和も同じ

　　　Aと B+8 から1個ずつ取った和とBと A+8 から1個ずつ取った和も同じ

　従って、A’とB’は条件を満たす。

　一般に、ｎ個の場合のＡとＢからＡ’とＢ’を次のように作る。

　　Ａ’＝A∪(B+m)　、Ｂ’＝B∪(A+m)　　（ただし、m は、A∪B の最大値より大きい数)

　但し書きは、Ａ’やＢ’が集合になるようにしたもので、もっと弱くてもよい。

　このとき、Ａ’とＢ’は、２ｎのときの解を与える。

　このことから、ｎが２の累乗のとき、A≠B　かつ　S(A)=S(B) をみたすA、Bが存在すること
がわかる。逆も成り立つらしいが、非常に難しいらしい。


　ＦＮさんからの続報です。（平成２３年８月３１日付け）

(４)　ｎ＝８　のとき、A≠B　かつ　S(A)=S(B)　をみたすA、Bを作れ。

について、

　　A＝{0，3，5，6，9，10，12，15}　、Ｂ＝{1，2，4，7，8，11，12，14}

以外にも解はいくらでもあります。しかし、上の解は、0 から 15 までの整数を２つの集合 A、
B にわけて、S(A)=S(B)が成り立つようにしたということで特別なものです。これを満たす A、
B は、(AとBをすべて入れ変えたものを除いて)１つしかありません。

　これは、次のように地道に調べていけば確認できます。

　0がＡに入るとする。
　1がＡに入ると、1+0=1がＢで作れないから、1はＢ
　2がＡに入ると、2+0=2がＢで作れないから、2はＢ
　3がＢに入ると、1+2=3がＡで作れないから、3はＡ
　4がＡに入ると、4+0=4がＢで作れないから、4はＢ
　5がＢに入ると、1+4=5がＡで作れないから、5はＡ
　6がＢに入ると、2+4=6がＡで作れないから、6はＡ
　7がＡに入ると、7+0=7がＡで作れないから、7はＢ

この段階で、　A＝{0，3，5，6}　、Ｂ＝{1，2，4，7}

　8がＡなら、Ａで0+8=3+5=8、Ｂでは、1+7=8だけだから、8はＢ
　9がＢなら、Ｂで1+8=2+7=9、Ａでは、3+6=9だけだから、9はＡ
　10がＢなら、Ｂで2+8=10、Ａではなしだから、10はＡ
以下同様。

　これは、次の形に一般化できます。

自然数 ｋ に対して、集合A、Bで次の条件を満たすものが一意的に存在する。

　(0)　0はＡに属する
　(1)　Ａ∩Ｂ＝φ
　(2)　Ａ∪Ｂ＝{0，1，2，・・・・，2^k-1}
　(3)　S(A)＝S(B) 　ただし、S(A)は、Ａから異なる２つを取り出して作った和のすべて

　これを証明してください。存在は前に書いた要領でできます。あとは一意性です。

上のA、Bを２進法で書くと次のようになります。

　　　　A＝{0，11，101，110，1001，1010，1100，1111}

　　　　B＝{1，10，100，111，1000，1011，1101，1110}

即ち、Aは、２進法で書いたときに、1の個数が偶数であるものの全体であり、Bは、２進法で
書いたときに、1の個数が奇数であるものの全体です。

　一般の場合(0から2^k-1までの場合)も成り立つことは作り方から直ぐわかります。もちろん
一意性が証明できたとしてですが．．．。



　　　以下、工事中