
当HPがいつもお世話になっているHN「よおすけ」さんからの出題です。
(平成30年10月23日付け)
62□□427が99で割り切れるように、□□を補充せよ。
(答) □□=24
問題の式を、筆算で表すと以下のようになる。
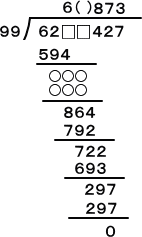
( )が3のとき、○○○ ○○○ には、383 297 がそれぞれ入り、□□=23 となり、
383−297=86 は成り立つが、622−594=28 と、38にはならないため、不適。
( )が2のとき、○○○ ○○○ には、284 198 がそれぞれ入り、□□=24 となり、
284−198=86 、622−594=28 が共に成り立つため、適する。
62□−594の十の位の候補は、2または3のため、( )内が0、1および4以上の場合は
確かめなくて良い。
□□=24 のとき、62□□427=622427 となり、622427÷99=62873
よって、求める答えは、□□=24 である。
(コメント) 別解を考えてみました。
62AB427が99で割り切れることから、62AB427は、9でも11でも割り切れる。
まず、6+2+A+B+4+2+7=A+B+21 が9の倍数から、 A+B=6、15
6−2+A−B+4−2+7=A−B+13 が11の倍数から、 A−B=−2、9
よって、(A+B,A−B)=(6,−2)、(6,9)、(15,−2)、(15,9)
このうち、2Aが奇数となる(6,9)、(15,−2)は不適。
2Aが18を超える(15,9)は不適。
よって、(A+B,A−B)=(6,−2)のとき、 A=2、B=4 が求める解。