倍々問題　　　　　　　　 　　　　　　　　　　　　　　　　　　　　

今、２点 Ａ、Ｂ を結ぶ線分がある。右下図のように、次のような手順で、棒を次々に立てて いく。
線分ＡＢの中点Ｍ1に、長さ １ の棒を 立てる。 　線分ＡＭ1、Ｍ1Ｂの中点Ｍ21、Ｍ22に、 長さ ２ の棒を立てる。 　線分ＡＭ21、Ｍ21Ｍ1、Ｍ1Ｍ22、Ｍ22Ｂ の中点Ｍ31、Ｍ32、Ｍ33、Ｍ34に、長さ ４ の棒を立てる。 以下同様にして、各線分の中点に、直前 に立てた棒の長さの２倍の長さをもつ棒 を立て、長さが ５１２ の棒を立てたところ で、この作業を止める。
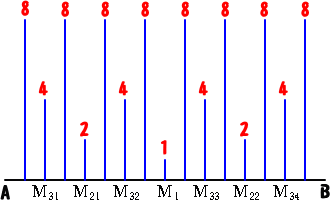このとき、Ａ側から数えて、ちょうど ５００番目に立つ棒の長さは、いくらだろうか？

（参考文献：ピーター・フランクル　著　ピーター先生と中学入試の算数に挑戦！（新潮社））










（答）　長さ ｎ の棒は、ｎ 本あるので、棒は全部で、 １＋２＋４＋８＋・・・＋５１２＝１０２３ 本
　　　ある。これは、次のように考えても良い。
　　　　最後に立てた長さ ５１２ の棒は、５１２ 本あり、これらは、奇数番（１、３、・・・）に並ぶ。
　　　よって、５１２ 番目の奇数は、自然数列において、２×５１２−１＝１０２３ 番目となるの
　　　で、棒の総数は、１０２３ 本である。
　　　　ところで、長さ ５１２ の棒を立てる前の状態、すなわち、２５６ 本の、長さ ２５６ の棒は、
　　　奇数番（１、３、５、・・・、５１１）にあるわけが、これに、長さ ５１２ の棒を立てると、長さが
　　　２５６ の棒は、２×１、２×３、・・・、２×５１１番目に並ぶことになる。
　　　　同様にして、１２８ 本の、長さ １２８ の棒は、最初、奇数番（１、３、５、・・・、２５５）に並
　　　ぶが、長さ ２５６ の棒、長さ ５１２ の棒を追加することにより、その並ぶ順番は、
　　　４×１、４×３、４×５、・・・、４×２５５番目となる。
　　　　ここで、５００＝４×１２５ （１２５ は奇数）なので、５００番目に立つ棒の長さは、１２８
　　　となる。

　　　（この問題は、最後の状態から考えて、順次直前の状態を考慮するのが、ポイント！
　　　　一般に、ｎ 番目の棒の長さを求めるには、次のようにすればよい。
　　　　ｎ ＝２^ｋ×（奇数）となる ｋ を求めて、５１２÷２^ｋ を計算する。その答が、棒の長さ）