嶰嶳曵偟僎乕儉丂丂 丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
丂壓恾偺傛偆偵丄俁峴偺栚偐傜側傞斦偑偁傝丄俁偮偺峴偺忋偵俁偮偺嬵偑抲偄偰偁傞丅
丂丂丂丂丂丂丂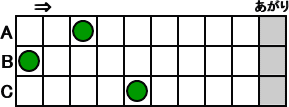
丂俀恖偺僾儗僀儎乕偑岎屳偵丄揔摉側侾偮偺嬵傪揔摉側悢偺栚偩偗塃偵偢傜偟偰偄偔丅
偁偑傝偺栚偺忋偺嬵偼丄偦傟埲忋塃偵摦偐偣側偄傕偺偲偡傞丅
丂嵟屻偵丄嬵傪摦偐偟偨幰傪彑偪偲偡傞丅
丂幚嵺偵丄俥倢倎倱倛 偱丄嬵傪摦偐偟偰梀傫偱傒傛偆両
丂丂俥倢倎倱倛 斉偼丄偙偪傜丂丂丂丂俫俿俵俴 斉偼丄偙偪傜丂丂傪僋儕僢僋偟偰偔偩偝偄丅
丂僙僉儏儕僥傿曐岇偺偨傔丄僐儞僺儏乕僞偵傾僋僙僗偱偒傞傾僋僥傿僽丂僐儞僥儞僣偑昞帵偝傟側偄傛偆偵丄
俬値倲倕倰値倕倲丂俤倶倫倢倧倰倕倰丂偱惂尷偟偰偄傞偲丄俫俿俵俴斉丄俥倢倎倱倛斉偲傕偵尒傜傟傑偣傫丅僽儘僢僋偝傟偰偄傞
僐儞僥儞僣傪嫋壜偟偰偔偩偝偄丅乮偡傒傑偣傫丄帺屓偺愑擟偱偍婅偄偟傑偡丅乯
丂偙偺僎乕儉偼丄俁偮偺嶳偵愊傑傟偨峝壿傪岎屳偵庢偭偰偄偒丄嵟屻偺峝壿傪庢偭偨傕偺
偑彑偪偲偡傞乽嶰嶳曵偟乿偺堦偮偺曄宍僶乕僕儑儞偱偁傞丅
丂忋婰偺僎乕儉偼丄嬵偺攝抲偐傜丄幚偼乽愭庤昁彑乿偺僎乕儉偵側偭偰偄傞丅乽愭庤昁彑乿
偲偼丄傕偪傠傫乽愭庤偑惓偟偔墳懳偡傟偽丄昁偢彑偮偙偲偑偱偒傞乿偲偄偆堄枴偱偁傝丄愭庤
側偺偵丄岆偭偨墳懳傪偡傟偽丄摉慠彑偮偙偲偼偱偒側偄丅
丂偝偰丄偙偺愭庤昁彑偺僎乕儉偱愭庤偑妋幚偵彑偮偨傔偵丄偳偺傛偆側墳懳傪偡傟偽偄偄
偩傠偆偐丠
丂偙偺峌棯偵偼丄惍悢榑偲偄偆悢妛偑梡偄傜傟傞丅
丂崱丄惍悢倃傪丄俀恑朄揥奐偟偰丄
丂丂丂丂丂倃亖倃0俀値亄倃1俀値亅1亄倃2俀値亅2亄丒丒丒亄倃値亅侾俀亄倃値
偲昞偡丅偙偺偲偒丄偦偺學悢傪敳偒弌偟偰丄弴彉懳
丂丂丂丂丂丂丂乮倃0丆倃1丆倃2丆丒丒丒丆倃値亅侾丆倃値乯
傪峫偊傞丅
丂忋婰偺椺偵偍偄偰丄俙偺峴偵偁傞嬵偼丄偁偑傝傑偱丄嬵傪俈偮恑傔側偗傟偽側傜側偄丅
偙偺偙偲傪丄俙佭俈偲昞偡丅俈亖侾亊俀2亄侾亊俀亄侾丂側偺偱丄弴彉懳乮侾丆侾丆侾乯偑掕傑傞丅
摨條偵偟偰丄俛佭俋丄俠佭俆丂傛傝丄偦傟偧傟弴彉懳乮侾丆侽丆侽丆侾乯丄乮侾丆侽丆侾乯偑掕傑傞丅
丂挿偝偺堎側傞弴彉懳傪丄愭摢偵侽傪偄偔偮偐壛偊傞偙偲偵傛偭偰丄摨偠挿偝偺弴彉懳偵
曄宍偡傞偙偲偑偱偒傞丅
丂偙偺傛偆偵偟偰丄俙丄俛丄俠偺奺峴偵懳偟偰丄師偺傛偆側弴彉懳偑懳墳偡傞丅
丂丂丂丂俙佭乮侽丆侾丆侾丆侾乯丂丂丂丂俛佭乮侾丆侽丆侽丆侾乯丂丂丂丂丂俠佭乮侽丆侾丆侽丆侾乯
丂偙偙偱丄俙丄俛丄俠丂偦傟偧傟偺侾斣栚丄俀斣栚丄俁斣栚丄係斣栚偺悢偺榓傪丄弴彉懳
丂丂丂丂丂丂丂丂丂丂丂丂丂丂乮俹丆俻丆俼丆俽乯
偱昞偡丅
丂俹亖侽亄侾亄侽亖侾丄俻亖侾亄侽亄侾亖俀丄俼亖侾亄侽亄侽亖侾丄俽亖侾亄侾亄侾亖俁丂側偺偱丄
弴彉懳偼丄乮侾丆俀丆侾丆俁乯偲側傞丅
丂GAME OVER丂偺偲偒丄偙偺弴彉懳偼丄乮侽丆侽丆侽丆侽乯偲側傞丅
丂偟偨偑偭偰丄弴彉懳乮侾丆俀丆侾丆俁乯偐傜弴彉懳乮侽丆侽丆侽丆侽乯偵曄慗偟偰偄偔夁掱偺拞偱丄
愭庤偑偳偺傛偆側愴棯傪偲傟偽偄偄偺偐偲偄偆偙偲偵側傞丅
丂偙偺偲偒丄師偺帠幚偼廳梫偱偁傞丅
丂嬵偵堏摦偑偁偭偨応崌丄俀恑朄揥奐偺惈幙偐傜丄俙丄俛丄俠偺壗傟偐偵偍偄偰昁偢丄
偡偔側偔偲傕侾売強偵偍偄偰丄侽偐傜侾丄傑偨偼丄侾偐傜侽丂偺曄壔偑偁傞丅
丂偙偺偲偒丄俹丄俻丄俼丄俽偺嬼悢丒婏悢偑曄壔偡傞丅
丂傛偭偰丄愭庤偼丄俹丄俻丄俼丄俽慡偰偑嬼悢偱偁傞忬懺偱丄屻庤偵庤傪搉偣偽丄昁偢彑偮
偙偲偑偱偒傞丅
丂側偤側傜丄屻庤偼丄俙丄俛丄俠偺壗傟偐偱嬵傪摦偐偡偲丄俹丄俻丄俼丄俽偺彮側偔偲傕堦偮偼
昁偢婏悢偲側傝丄慡偰偑嬼悢偺嵟屻偺弴彉懳乮侽丆侽丆侽丆侽乯偵偼摓払偟偊側偄偐傜偱偁傞丅
丂埲忋偺偙偲傪擮摢偵偍偄偰丄愭庤昁彑偺庤弴椺傪帵偦偆丅屻庤偺懳墳偼丄僎乕儉偑憗偔
廔傢傞傛偆偵偟偰偁傞丅
| 丂 |
愭丒屻 |
俙 |
俛 |
俠 |
俹俻俼俽 |
庤丂丂丂弴 |
| 侽 |
巒傔 |
侽侾侾侾 |
侾侽侽侾 |
侽侾侽侾 |
侾俀侾俁 |
丂 |
| 侾 |
愭庤 |
丂 |
侽侽侾侽 |
丂 |
侽俀俀俀 |
俛偺峴偺嬵傪俈偮恑傔傞 |
| 俀 |
屻庤 |
侽侽侽侽 |
丂 |
丂 |
侽侾侾侾 |
俙偺峴偺嬵傪俈偮恑傔傞 |
| 俁 |
愭庤 |
丂 |
丂 |
侽侽侾侽 |
侽侽俀侽 |
俠偺峴偺嬵傪俁偮恑傔傞 |
| 係 |
屻庤 |
丂 |
侽侽侽侽 |
丂 |
侽侽侾侽 |
俛偺峴偺嬵傪俀偮恑傔傞 |
| 俆 |
愭庤 |
丂 |
丂 |
侽侽侽侽 |
侽侽侽侽 |
俠偺峴偺嬵傪俁偮恑傔傞 |
丂忋婰偺僎乕儉偼丄俹丄俻丄俼丄俽偺弶婜偺忬懺偑丄乽彮側偔偲傕堦偮偼婏悢乿偩偭偨偺偱丄愭
庤昁彑偱偁偭偨丅傕偟丄俹丄俻丄俼丄俽偺弶婜偺忬懺偑丄乽慡偰嬼悢乿偺応崌偼丄屻庤昁彑偲側
傞丅傑偨丄愭庤昁彑偺僎乕儉偱屻庤傪傂偄偰傕丄忋婰偺棟榑偑暘偐偭偰偄傞偁側偨偼丄愭
庤偺岆偭偨懳墳偑捈偖暘偐傝丄彑棙偵揮偠傞婡夛傕憹偊傞偼偢偱偁傞丅
丂傑偨丄忋婰棟榑偵偍偄偰丄乽俙丄俛丄俠偺俁峴乿偲偄偆偙偲偵杮幙揑側堄枴偼側偄丅幚偼丄壗
峴偁偭偰傕丄忋婰棟榑偼惉棫偡傞丅
丂楙廗栤戣偲偟偰丄係峴偺応崌傪壓婰偵宖帵偟偰偍偔丅嫵幒偺崟斅側偳偱丄媺桭傪憡庤偵
惀旕丄偙偺棟榑偑惓偟偄偙偲傪幚徹偟偰傒偰梸偟偄丅
丂丂丂丂丂丂丂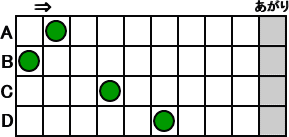
丂埲壓偵丄愭庤昁彑偺庤弴傪帵偟偰偍偔丅乮屻庤偺懳墳偼丄僎乕儉偑憗偔廔傢傞傛偆偵愝掕乯
| 丂 |
愭丒屻 |
俙 |
俛 |
俠 |
俢 |
俹俻俼俽 |
庤丂丂丂弴 |
| 侽 |
巒傔 |
侾侽侽侽 |
侾侽侽侾 |
侽侾侾侽 |
侽侾侽侽 |
俀俀侾侾 |
丂丂 |
| 侾 |
愭庤 |
丂丂 |
丂 |
侽侾侽侾 |
丂 |
俀俀侽俀 |
俠傪侾偮 |
| 俀 |
屻庤 |
丂 |
侽侽侽侽 |
丂丂 |
丂 |
侾俀侽侾 |
俛傪俋偮 |
| 俁 |
愭庤 |
侽侽侽侾 |
丂丂 |
丂 |
丂 |
侽俀侽俀 |
俙傪俈偮 |
| 係 |
屻庤 |
丂丂 |
丂 |
丂 |
侽侽侽侽 |
侽侾侽俀 |
俢傪係偮 |
| 俆 |
愭庤 |
丂丂 |
丂丂 |
侽侽侽侾 |
丂 |
侽侽侽俀 |
俠傪係偮 |
| 俇 |
屻庤 |
侽侽侽侽 |
丂 |
丂 |
丂 |
侽侽侽侾 |
俙傪侾偮 |
| 俈 |
愭庤 |
丂 |
丂 |
侽侽侽侽 |
丂 |
侽侽侽侽 |
俠傪侾偮 |
丂忋婰偺僎乕儉偱偼丄嬵偼帺桼偵岲偒側偩偗摦偐偡偙偲偑偱偒偨偑丄杮棃偺乽嶰嶳曵偟乿偵
偍偄偰偼丄嬵偺摦偒偵惂尷傪壛偊傞偙偲偑懡偄丅
丂壓恾偺傛偆偵丄俁峴偺栚偐傜側傞斦偑偁傝丄俁偮偺峴偺忋偵俁偮偺嬵偑抲偄偰偁傞丅
丂丂丂丂丂丂丂
丂俀恖偺僾儗僀儎乕偑岎屳偵丄揔摉側侾偮偺嬵傪侾偮偐俀偮偐俁偮偺栚偩偗塃偵偢傜偟偰偄
偔丅偁偑傝偺栚偺忋偺嬵偼丄偦傟埲忋塃偵摦偐偣側偄傕偺偲偡傞丅
丂嵟屻偵丄嬵傪摦偐偟偨幰傪彑偪偲偡傞丅
丂偙偺傛偆側僎乕儉偺応崌丄偙傟偼愭庤昁彑偲尵偊傞偱偁傠偆偐丠
丂俙丄俛丄俠 偵偍偄偰丄偁偑傝偺栚傑偱偺栚偺屄悢偑丄偦傟偧傟 倎丄倐丄們 偺偲偒偺嬵偺忬懺
傪 乮倎丄倐丄們乯偱昞偡偙偲偵偡傞丅
丂嬵偺忬懺偑師偺応崌偵屻庤偑偳偆嬵傪摦偐偟偰傕愭庤偑彑偰傞偙偲偼柧傜偐偱偁傠偆丅
丂丂丂丂丂乮侽丄侾丄侾乯丂丄丂乮侽丄俀丄俀乯丂丄丂乮侽丄俁丄俁乯丂丄丂乮侾丄俀丄俁乯
丂側偤側傜丄弴彉懳偑偦傟偧傟 乮侽丆俀乯乮俀丆侽乯乮俀丆俀乯乮俀丆俀乯偱丄壗傟傕嬼悢偱偁傞偐傜偱
偁傞丅
丂偟偨偑偭偰丄愭庤昁彑偲側傞偨傔偵偼丄忋婰偺傛偆側嬵偺忬懺偵偟偰屻庤偵庤傪搉偣偽
傛偄丅
丂偲偙傠偱丄屻庤偑摦偐偟偨栚偺悢偵懳偟偰丄摨偠嬵偱懌偟偰係偲側傞傛偆偵愭庤偑懳墳偡
傟偽丄昁偢摨偠僷僞乕儞偑孞傝曉偝傟傞丅乮偨偩偟丄摦偐偡慜偺栚偺悢偼係埲忋丅乯
丂偟偨偑偭偰丄嬵偺忬懺傪
丂丂丂丂乮係倠丄係倣亄侾丄係値亄侾乯丂丂丄丂丂乮係倠丄係倣亄俀丄係値亄俀乯
丂丂丂丂乮係倠丄係倣亄俁丄係値亄俁乯丂丂丄丂丂乮係倠亄侾丄係倣亄俀丄係値亄俁乯
偱偁傞傛偆偵偟偰屻庤偵庤傪搉偡偙偲偑偱偒傟偽丄愭庤昁彑偱偁傞丅
丂偝偰丄忋婰偺恾偵偍偄偰丄嬵偺忬懺偼丄乮俈丄俋丄俆乯偱偁傞丅偡側傢偪丄
丂丂丂丂丂丂丂乮俈丄俋丄俆乯亖乮係丒侾亄俁丄係丒俀亄侾丄係丒侾亄侾乯
側偺偱丄俙偺嬵傪俁偮偩偗摦偐偡偲丄乮係倠丄係倣亄侾丄係値亄侾乯偺僞僀僾偵偟偰屻庤偵庤傪
搉偡偙偲偑偱偒傞丅
丂偟偨偑偭偰丄愭庤昁彑偲偄偊傞丅
乮嶲峫暥專丗傾丒儎僌儘儉丄僀丒儎僌儘儉 挊丂丂摏堜岶堺 栿
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂弶摍揑偵夝偄偨崅摍悢妛偺栤戣乮嘨乯乮搶嫗恾彂乯
丂丂丂丂丂丂丂摗懞岾嶰榊丄揷懞嶰榊丂挊丂悢妛楌巎僷僘儖丂丂乮島択幮乯乯


