
当HPがいつもお世話になっているHN「らすかる」さんからの出題です。
(平成25年11月26日付け)
F(x)=x6+x+1 の最小値が 5/12 より大きいことを示せ。
(答) グラフ描画ソフトGrapesを用いて、グラフを描いてみた。
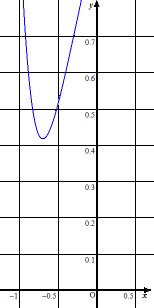
グラフから、最小値は、「0.418」位と分かるのだが、
5/12=0.41666・・・・
を考えると、相当に微妙ですね。
当HPの常連さんからは、正攻法で解ける問題を、なぜ、あのらすかるさんが...という出
題の意図を問う声が大きいですね!
らすかるさんによれば、「正攻法だと、手計算で5/12より大きいことを確認するのが大変で
す。電卓など使わず、複雑な手計算も不要な、エレガントな解法を期待しています。」とのこと
です。
空舟さんが考察されました。(平成25年11月26日付け)
y=x6+x+1 より、y'=6x5+1 なので、x=(-1/6)^(1/5) で最小値をとるので、
その時のyの値:5/6 * (-1/6)^(1/5) + 1> 5/12 を示せば良い。
5/6*(-1/6)^(1/5) > -7/12 を示せば良い。
(-1/6)^(1/5) > -7/10 を示せば良い。
(1/6)^(1/5) < 7/10 を示せば良い。
1/6 < (7/10)^5 を示せば良い。
10^5 < 6*7^5 を示せば良い。
ここで、 6*7^5 = 42*2401 で、 42*24 = 960 + 48 > 1000 から言える。
上記のように考えました。エレガントかどうかは分からないですが...。
(コメント) 空舟さんとほとんど同じですが、ちょっと解いてみました。
G(x)=x6+x+1−5/12=x6+x+7/12 とおくと、
G’(x)=6x5+1=0 はただ一つの解α(α<0)を持ち、x=αで極小かつ最小。
最小値は、G(α)。 6α5+1=0 のとき、G(α)=α6+α+7/12=(5/6)α+7/12
そこで、 αと−7/10 の大小関係を調べる。その大小関係は、α5と(−7/10)5 の大小
関係と同値である。すなわち、6α5+1(=0) と 6・(−7/10)5+1 の大小関係と同値。
6・(−7/10)5+1=−1.00842+1=−0.00842(<0)
よって、 6α5+1(=0)>6・(−7/10)5+1 すなわち、 α5>(−7/10)5 から
α>−7/10 が成り立ち、よって、 (5/6)α+7/12>0 であることが分かる。
以上から、 F(x)=x6+x+1 > 5/12 が成り立つ。
らすかるさんからのコメントです。(平成25年11月26日付け)
用意していた解答は、
x6+x+1 = (x2+1)(x2−1/2)2+(3/4)(x+2/3)2+5/12 > 5/12
でした。(→ 参考1、参考2)
GAI さんからのコメントです。(平成25年11月27日付け)
らすかるさんのアイデアを借りると(いつもハットするアイデアに感嘆)
一般に、nを正数にすると、
F(x)=x6+kx+c=(x2+n)(x2-n/2)2+(3/4)(nx+2k/(3n))2+{c-(n3/4+k2/(3n2))}
と変形できるので、F(x) の最小値は、 {c-(n3/4+k2/(3n2))}
ここで、G(n)=n3/4+k2/(3n2) と置くと、G(n)の最小値は相加平均、相乗平均から
2√(n3/4)・(k2/(3n2))=√(n/3)・|k|
なので、F(x) の最小値は、c-√(n/3)・|k| より大きいとしてはいけませんか?
らすかるさんからのコメントです。(平成25年11月27日付け)
F(x)=x6+kx+c=(x2+n)(x2-n/2)2+(3/4)(nx+2k/(3n))2+{c-(n3/4+k2/(3n2))}
という式から言えるのは、{c-(n3/4+k2/(3n2))} より大きい」です。
なぜなら、一般に、「(x2-n/2)2」と「(nx+2k/(3n))2」は同時に0にならないからです。