最大値2 
当HPがいつもお世話になっているHN「よおすけ」さんからの出題です。
(令和4年5月1日付け)
下図のように、底辺の長さが6、斜辺の長さが5の二等辺三角形ABCがあり、その三角形
に長方形PQRSが内接している。この長方形の面積Tの最大値を求めよ。
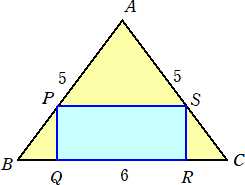
(答) 下図のように、二等辺三角形ABCを座標平面に埋め込む。
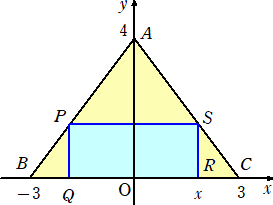
直線ACの方程式は、 y=(−4/3)x+4 なので、S(x,(−4/3)x+4) である。
このとき、面積T=2x((−4/3)x+4)=(−8/3)x2+8x ただし、 0<x<3
平方完成して、 T=(−8/3)(x−3/2)2+6 となるので、
Tは、x=3/2 のとき最大で、最大値 6 である。 (終)
りらひいさんからのコメントです。(令和4年5月2日付け)
以下の話はどこかで既出かもしれませんが……、概要のみ書きます。
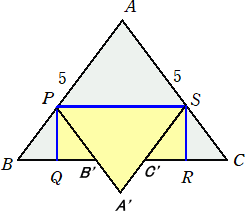
△ABCの形に切った紙を用意し、直線PS、PQ、SRで紙を折り返すことで、3つの△APS、
△PBQ、△CSRの面積の合計と長方形PQRSの面積を比較する。
折った後の紙の先端A、B、Cの位置をA’、B’、C’とする。
 |
|
 |
(あ) A’が長方形PQRSの内部にあるとき、折った後の3つの三角形は、長方形全体を覆っ
ていて、かつ、長方形の内側で紙が二重になっているところがある。
・・・(A’、B’、C’を結んだ内側の領域)
また、B’近辺やC’近辺が長方形の外部に出る場合もある。
よって、3つの三角形の面積の合計は、長方形の面積より大きい。
すなわち、長方形PQRSの面積は、元の三角形ABCの面積の半分より小さい。
(い) A’が線分QR上にあるとき、A’、B’、C’は同じ点となり、折った後の3つの三角形を合
わせるとちょうど長方形と一致する。
よって、3つの三角形の面積の合計は、長方形の面積と等しい。
すなわち、長方形PQRSの面積は、元の三角形ABCの面積の半分である。
(う) A’が長方形PQRSの外部にあるとき、折った後の3つの三角形は、長方形全体と長方
形外部にできる△A’B’C’を合わせたものである。
よって、3つの三角形の面積の合計は、長方形の面積より大きい。
すなわち、長方形PQRSの面積は、元の三角形ABCの面積の半分より小さい。
(あ)、(い)、(う)より、長方形の面積が最大になるのは、(い)の場合である。このときの長方
形PQRSの面積は三角形ABCの面積の1/2である。
あとは、何らかの方法で、△ABCの面積がわかればよい。
#きちんとした解答にするためには、
・折り紙ではなく、線対称な点として議論する。
・点Pにおける角度の議論から、3点P、A’、B’が一直線上にあることを示す。
3点S、A’、C’も同様。
・面積の不等式を作るために、図形をちゃんと分割する。
などが必要で、結構面倒くさいです。
なお、この方法は、∠B、∠Cが鋭角ならばどんな三角形でも使えます。
(コメント) 視覚的に、最大になる瞬間が見えそうですね!りらひいさんに感謝します。
らすかるさんからのコメントです。(令和4年5月3日付け)
二等辺三角形ABCの高さを変えずBCをk倍に長くすると、長方形の面積もk倍になるから、
BCの長さを変えても長方形の面積が最大になるときの長方形の高さは変わらない。
∠Aが直角(すなわち、BC=8 で二等辺三角形ABCが直角二等辺三角形)の場合を考え、
BCに関して、A、P、S と対称な点をA’、P’、S’とすると、長方形PP’S’Sの周の長さは一
定(16)なので、長方形PP’S’Sの面積が最大(⇔長方形PQRSの面積が最大)になるのは
長方形PP’S’Sが正方形になるときで、この面積は、16。
長方形PQRSの面積は、この半分で、さらに、BCを4/3倍に伸ばしたので、3/4倍にして、
元の長方形PQRSの面積の最大値は、16÷2×(3/4)=6
(コメント) 周の長さ一定な長方形を作るために、直角二等辺三角形を考えるんですね。
新しい見方・考え方です。らすかるさんに感謝します。
以下、工事中!



