当ＨＰの読者の方より、マッチ棒問題を頂きました。（平成２４年１月１３日付け）
解き方を忘れてしまい、とても気になっている問題があります。
それぞれの辺が５本、１２本、１３本のマッチ棒からなる直角三角形を作ります。このとき、
新たな１０本のマッチ棒を用いて、この面積を三等分するにはどうすればいいでしょうか？
昔解いて、その解き方を忘れてしまいました。確か、三角形の内接円を書いて解いた気が
します。（その方法でなくてもかまいません。）
もし、お時間がありましたら、ぜひ考えていただきたいです。
（答） 読者の方のヒントを参考に考えてみました。
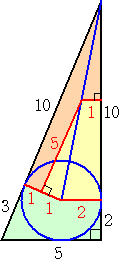
内接円の半径 ｒ は、 １３−（１２−ｒ）＋ｒ＝５ より、 ｒ＝２このとき、内接円の中心を用いて、三角形の面積＝３０ は、左図の
ような分割で、それぞれ面積が１０ の図形に分割される。
しかし、この分割では、「マッチ棒を１０本用いる」という条件に適さ
ない。
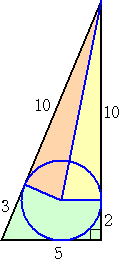
そこで、合同な三角形を交換する考え方で、次のような分割を行う
と、「マッチ棒を１０本用いる」という条件に適する。
