
当HPがいつもお世話になっているHN「GAI」さんからの出題です。
(平成27年9月3日付け)
平面上に異なる6本の線分を引くとき、これらの線分の端点として得られる点の中で、異な
る点は最小限何個できるか?
また、100本の線分なら何個になるか?
(コメント) 平面上に異なる6本の線分を引くとき、次の図から4点でいいのかな?
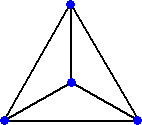
DD++さんが考察されました。(平成28年9月26日付け)
n個の点があると、線分は、n(n-1)/2 本まで引けます。つまり、線分6本なら点は最少4個、
線分100本なら点は最少15個。
(コメント) なるほど、逆算すれば分かるのですね!