素朴な長さの計算２ 　　　　　　　　　　　　　　　　　　　　　　　　　

　AB＝２４、AD＝３６の長方形ABCDがある。AB上にEB＝５となる点ＥとＡＤ上に点Ｇをとり、
線分EGで長方形を折り返し、交点Fに対して、ＢＦ＝１２、ＦＡ＝６とする。

　　　　　　

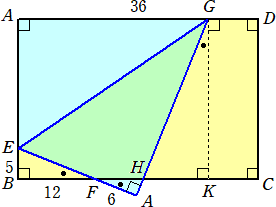
　このとき、次の線分の長さ、面積を求めよ。

(1)　ＣＨ　　(2)　AG　　(3)　台形ＧＨＣＤの面積











































（答）（１）　EF＝１３　で、△FBE∽△FAH　より、　FH＝１３/２

　　　　　よって、　CH＝３６−（１２＋１３/２）＝３５/２

（２）　ＨＫ＝２４×（５/１２）＝１０　より、

　　　ＧＨ²＝ＨＫ²＋ＧＫ²＝１００＋５７６＝６７６＝２６²　より、　ＧＨ＝２６

　　ここで、　ＨＡ＝６×（５/１２）＝５/２　なので、　ＡＧ＝２６＋５/２＝５７/２

（３）　ＧＤ＝ＣＫ＝３５/２−１０＝１５/２　より、

　　台形ＧＨＣＤの面積＝（１５/２＋３５/２）×２４÷２＝２５×１２＝３００