
当HPがいつもお世話になっているHN「GAI」さんからの出題です。
(令和元年6月22日付け)
問題 △ABCに対し、辺ABをα:βに内分する点をD、辺ACをm:nに内分する点をEとし、
CDとBEが交わる交点をP、AとPを結んだ線が辺BCと交わる点をQとする。
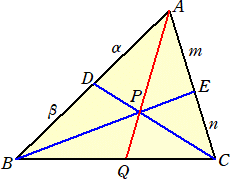
このとき、 (1) AP:PQ (2) BQ:QC を求めよ。
(答) カナさんから解答をいただきました。(令和元年6月22日付け)
メネラウスの定理を用いず他の自然な方法で、
(1) AP:PQ=mβ+nα:nβ (2) BQ:QC=mβ:nα
これで大丈夫のようです。
らすかるさんが考察されました。(令和元年6月22日付け)
△ABQと直線CDに関するメネラウスの定理により、
α/β・(BQ+QC)/QC・PQ/PA=1 … (a)
△AQCと直線BEに関するメネラウスの定理により、
m/n・(BQ+QC)/BQ・PQ/PA=1 … (b)
(a)/(b) から、 BQ/QC=(mβ)/(nα) … (c)
(c)から、(BQ+QC)/QC=(mβ+nα)/(nα) なので、(a)に代入して整理すると、
AP/PQ=(mβ+nα)/(nβ)
従って、 (1) AP:PQ=mβ+nα:nβ (2) BQ:QC=mβ:nα
#ちなみに他の内分比は、 CP:PD=n(α+β):mβ 、BP:PE=(m+n)β:nα
(コメント) ベクトルにおける定型的な線分比の計算ですね。
私だったら、チェバの定理から、BQ:QC を求め、その後、メネラウスの定理を用いて、
AP:PQ を求めるのかな...。
実際に、 (α/β)・(BQ/QC)・(n/m)=1 から、 BQ/QC=(mβ)/(nα)
(α/β)・(mβ+nα)/(nα)・(PQ/AP)=1 から、 PQ/AP=(nβ)/(mβ+nα)
# カナさんは、ベクトルの一次独立の性質を用いて求められたのかな?
カルピスさんからのコメントです。(令和元年6月22日付け)
以前にも載せたサイト「メネラウスとチェバの定理の超進化系!」だけど、アゲイン。