線分の長さ　　　　 　　　　　　　　　　　　 　　　　　　　　　　　　　　　

　当ＨＰがいつもお世話になっているＨＮ「Ｓ（Ｈ）」さんからの出題です。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（平成２９年９月２１日付け）

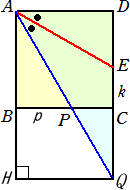
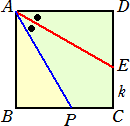
問題　一辺が１２の正方形ABCDの辺BC上に点Pをとり、∠PADの２等分線が辺CDと交わ
　　　　る点をE、CE＝ｋ であるとき、線分APの長さを求めよ。

　　　
































（答）　スモークマンさんが考察されました。（平成２９年９月２１日付け）

　∠ＤＡＥ=θとすると、　tanθ=(12-k)/12　より、

　　　tan(2θ)=((12-k)/6)/(1-(1-k/12)^2)=24(12-k)/(k(24-k))

　ＢＰ=ｐ　として、　p/12=(12-p)/(12*24(12-k)/(k(24-k))-12)　より、p=k(24-k)/(2(12-k))

　よって、　AP²=12²+p²　なので、

　AP=(12^2+(k(24-k)/(2(12-k))^2)^(1/2)=(1/2)√((12/(12-k))^2+575)

かなぁ…^^。


（コメント）　スモークマンさんが三角比を用いて解かれましたが、次のように角の２等分線の
　　　　　　性質を用いる方法も考えられます。

　下図で、△ＡＢＰ∽△ＱＣＰ　より、１２ ： ｐ＝ＱＣ ： １２−ｐ　なので、ＱＣ＝１２(１２−ｐ)/ｐ

また、　ＡＰ＝√（ｐ2＋１４４）　で、△ＡＢＰ∽△ＡＨＱ　より、 　　　ＡＱ＝ＡＰ・（１２/ｐ）　すなわち、　ＡＰ＝ＡＱ・（ｐ/１２） 　　　線分ＡＥは∠ＱＡＤの２等分線なので、　ＡＱ ： ＡＤ＝ＱＥ ： ＥＤ 　　　よって、　ＡＱ ： １２＝１２(１２−ｐ)/ｐ＋ｋ ： １２−ｋ　より、 　　　　　ＡＱ＝（１４４(１２−ｐ)/ｐ＋１２ｋ）/（１２−ｋ）

以上から、

√（ｐ²＋１４４）＝（１４４(１２−ｐ)/ｐ＋１２ｋ）/（１２−ｋ）・（ｐ/１２）
　　　　　　　　　＝（１２(１２−ｐ)＋ｐｋ）/（１２−ｋ）

両辺を平方して整理すると、　（１２−ｋ）²（ｐ²＋１４４）＝（１２(１２−ｐ)＋ｐｋ）²

これを展開して、ｐについて解くと、　ｐ＝（ｋ²−２４ｋ）/（２（ｋ−１２））

　このとき、　ｐ²＋１４４＝（ｋ²−２４ｋ）²/（２（ｋ−１２））²＋１４４
　　　　　　　　　　　　　　＝（ｋ⁴ー４８ｋ³＋８６４ｋ²−６９１２ｋ＋４１４７２）/（２（ｋ−１２））²

で、ＡＰ＝√（ｐ²＋１４４）　が求められる。

＃未知数ｋを含んでいるので複雑な式に見えるが、例えば、ｋ＝４としてみるとスッキリした
　答えになる。因みに、ｋ＝４　のとき、ｐ＝５　で、そのとき、ＡＰ＝１３　となる。