
下図のように、円Oの外部にある点Aから中心Oを通る直線を引き、円Oとの交点をB、C
とする。円周上に点Dを∠DAC=30°となるようにとり、線分ADと円との交点をEとおく。
点Eにおいて線分ADに垂直な直線を引き、直径BCとの交点をFとおく。
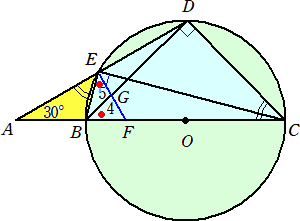
EG=5、GF=4 のとき、線分ABの長さを求めよ。
(答) AB=12
実際に、AF=18 で、AB=x とおくと、 BF=18−x である。
△BFG∽△EFB なので、 (18−x)/4=9/(18−x)
よって、 (x−18)2=36 から、 x−18=±6
AF>AB すなわち、 18>x なので、 x−18=−6 から、 x=12
よって、 AB=12 (終)
(コメント) 別解を募集中です!
以下、工事中!