素朴な長さの計算14　　　　　　　　　　　　　　　　　　　　　　　　　

　下図のように、頂角４５°の△ＡＢＣがあり、頂点Ａより、底辺ＢＣに垂線ＡＨを下ろす。

　　

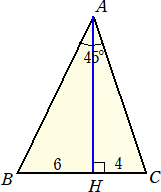
　ＢＨ＝６、ＨＣ＝４ のとき、線分ＡＨの長さを求めよ。
































（答）　ＡＨ＝１２

　実際に、ＡＨ＝ｘ とおくと、　ＡＢ＝√（ｘ²＋３６）　、ＡＣ＝√（ｘ²＋１６）

△ＡＢＣにおいて、余弦定理より、

　１００＝（ｘ²＋３６）＋（ｘ²＋１６）－２√（ｘ²＋３６）・√（ｘ²＋１６）・ｃｏｓ４５°

すなわち、　√（ｘ²＋３６）・√（ｘ²＋１６）＝２ｘ²－４８

両辺を平方して、　２（ｘ²＋３６）（ｘ²＋１６）＝４ｘ⁴－１９２ｘ²＋２３０４　から、

　ｘ⁴－１４８ｘ²＋５７６＝０　すなわち、　（ｘ²－４）（ｘ²－１４４）＝０

よって、　ｘ²＝４　、１４４　より、　ｘ＝２　、１２

ｘ＝２　とすると、　Ａ＝１３５°となるので、不適

したがって、求める線分ＡＨの長さは、　１２　　（終）


　この問題について、次のように考えれば、もっと平易に解くことができる。

（別解）　△ＡＢＨ≡△ＡＢＥ　、△ＡＣＨ≡△ＡＣＦ　となるように点Ｅ、Ｆをとる。

　　

　このとき、四角形ＡＥＧＦが正方形となるように、点Ｇをとることができる。

　ＡＨ＝ｘ とおくと、　ＢＧ＝ｘ－６　、ＧＣ＝ｘ－４　なので、三平方の定理より、

　（ｘ－６）²＋（ｘ－４）²＝１００

すなわち、　ｘ²－１０ｘ－２４＝０　より、　（ｘ＋２）（ｘ－１２）＝０

　よって、　ｘ＝１２　となり、求める線分ＡＨの長さは、　１２　　（終）


（コメント）　ＡＨ＝１２　のとき、下図は、どのような幾何的性質を有するか、よおすけさんに
　　　　触発されて考えてみた。（令和６年９月１７日付け）

　　

　ＡＨ＝１２　のとき、ＡＢ＝６、ＡＣ＝４　である。そこで、辺ＡＢ上に、ＡＤ＝ＤＣ となる
ように点Ｄをとる。

　このとき、ＡＣ＝４　で、△ＡＤＣは直角２等辺三角形から、ＡＤ＝ＤＣ＝４　となる。

このとき、　ＢＤ＝２　である。

　線分ＤＣと線分ＡＨの交点をＥとし、点Ｄより、辺ＢＣに垂線ＤＦを引く。

　　

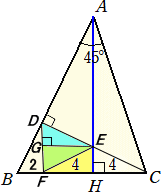
△ＤＢＦ∽△ＡＢＨ　で相似比は、１ ： ３ なので、ＡＨ＝１２　から、ＤＦ＝４　となり、したがって、

ＢＦ²＝（２）²－４²＝２０－１６＝４　から、ＢＦ＝２　すなわち、　ＦＨ＝４　となる。

△ＣＤＦにおいて、ＤＦとＥＨは平行で、Ｈは辺ＦＣの中点なので、中点連結定理より、

Ｅは辺ＤＣの中点となり、ＥＨ＝２　である。

したがって、△ＥＤＦは、ＥＤ＝ＥＦ　の２等辺三角形で、Ｅから辺ＤＦに下ろした垂線の足Ｇは

線分ＤＦの中点となる。

以上から、ＡＨ＝１２　すると、ＡＢ＝６、ＡＣ＝４　で、

　ＢＦ＝ＥＨ＝２、ＦＨ＝ＦＤ＝ＨＣ＝４、ＢＤ＝ＤＥ＝ＥＣ＝ＥＦ＝２

という美しい性質を持つことが分かった。


　kuiperbelt さんから別解をいただきました。（令和６年９月１７日付け）

　　

　∠ABC=θとして、AH＝ｘ＝６tanθ＝４tan(３π/４－θ)

　tanθ＝ｘ/６　、tan(３π/４－θ)＝ｘ/４　なので、

tan(３π/４－θ)＝(tan(３π/４)－tanθ)/(１＋tan(３π/４)tanθ)　より、

　x/４＝(－１－x/６)/(１－x/６)　であり、これより、

　x/４－x²/２４＝－１－x/６　から、x²－１０x－２４＝０　すなわち、　(x＋２)(x－１２)＝０

よって、x＝－２、１２　から、x＞０　なので、　AH＝x＝１２


（コメント）　kuiperbelt さん、別解をありがとうございます。現在、平面幾何的に「ＡＨ＝１２」
　　　　　が導けないか、思案中です。そのような解を得られた方、是非、ご教示ください。


　ｔａｎ を使う場合、次のような別解も考えられる。

（別解）　題意より、∠ＢＡＨ＝θ　とおくと、　ＡＨ・ｔａｎθ＝６　、ＡＨ・ｔａｎ（４５°－θ）＝４

よって、　２ｔａｎθ＝３ｔａｎ（４５°－θ）＝３・（１－ｔａｎθ）/（１＋ｔａｎθ）　から、

　２ｔａｎ²θ＋２ｔａｎθ＝３－３ｔａｎθ　すなわち、　２ｔａｎ²θ＋５ｔａｎθ－３＝０

　（２ｔａｎθ－１）（ｔａｎθ＋３）＝０　から、　ｔａｎθ＝１/２　、－３

０°＜θ＜４５°なので、　ｔａｎθ＝－３　は不適。

　したがって、ｔａｎθ＝１/２　となり、　ＡＨ＝６÷（１/２）＝１２　　（終）


　DD++ さんから別解をいただきました。（令和６年９月１９日付け）

　平面幾何的解法です。

　　

　この三角形の外心を O とすると、△OBC は OB＝OC の直角二等辺三角形である。

中心Ｏより、辺ＢＣに垂線ＯＤを下ろし、線分ＡＨに垂線ＯＥを下ろすと、

　ＢＤ＝５、ＯＤ＝ＥＨ＝５　より、外接円の半径は、ＯＢ＝ＯＡ＝５　なので、

　ＯＥ＝ＤＨ＝１　から、直角三角形ＯＡＥにおいて、三平方の定理より、

　ＡＥ²＝（５）²－１＝４９　なので、　ＡＥ＝７　となる。

以上から、　ＡＨ＝ＡＥ＋ＥＨ＝７＋５＝１２

と求まりますね。


（コメント）　DD++ さん、別解をありがとうございます。これまでとは違った視点による解法で
　　　　すね！



　　以下、工事中！