
下図のように、AB=ACの2等辺三角形ABCが円に内接している。円周上に点Dをとり、
直線ADと辺BCの交点をEとする。
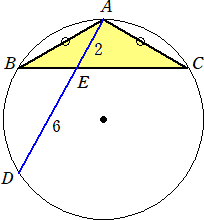
AE=2、ED=6 のとき、辺ABの長さを求めよ。
(答)

上図において、 △ABE∽△ADB より、 AB : AE=AD : AB なので、
AB : 2=8 : AB すなわち、 AB2=16 から、 AB=4 (終)
カルピスさんからのコメントです。(令和6年6月2日付け)
AB=4 と決まったところで、この円の半径を求めることは可能でしょうか。
らすかるさんからのコメントです。(令和6年6月2日付け)
AB=AC=4、∠ABC≦30°である二等辺三角形ABCを適当に描く。
∠ABC≦30°なので、BC上に、AE=2、∠AEB≧90°である点Eをとることができる。
このとき、△ABCの外接円を描いて、その円と直線AEとの交点のうち、Aでない方をDとする
と、DE=6 となる。
ということと同じですから、円の半径は「4以上」としか決まらず、求めることはできません。
カルピスさんからのコメントです。(令和6年6月2日付け)
らすかるさん、有難うございます。
一つだけ求める方法があります。それは、この図を正確に書いて、定規で測る。正確に書
けている自信はありませんが、約5ですね。
こんな方法も「有り」かな?計算で求めることが出来ないのなら、最後の手段。。。
(ブーイングが来そう(^^;)
(コメント) 問題の図を正確に書くことは難しいかもしれない。
カルピスさんからのコメントです。(令和6年6月3日付け)
この場合、半径は定まらなく、無数にあるのですね。
以下、工事中!