曲線の長さ２　　　 　　　　　　　　　　　　 　　　　　　　　　　　　　　　

　当ＨＰがいつもお世話になっているＨＮ「よおすけ」さんからの出題です。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（令和元年１１月１日付け）

問題　次の曲線の長さを求めよ。

(1)　9y^2=x(x-3)^2　の点(0,0)から点(3,0)までの部分

(2)　x=t^2、y=(1/3)t(t^2-3)　がx軸によって切りとられる部分




































（答）　ＧＡＩさんが考察されました。（令和元年１１月１日付け）

　答えは、(1)　4　(2)　2　かな？


　よおすけさんからのコメントです。（令和元年１１月１日付け）

　(2)で、yの式の両辺を2乗すると、y^2=(1/9)(t^2)(t^2-3)^2

　t^2=x　より整えると、　9y^2=x(x-3)^2　となります。


（コメント）　ＧＡＩさんの計算が（？）になっていたので、私も計算してみました。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（令和元年１１月６日付け）

　（１）の　9y^2=x(x-3)^2　のグラフは下図のようになります。



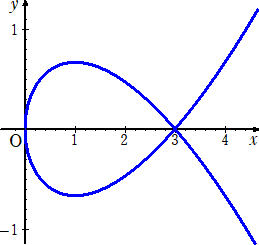
　9y^2=x(x-3)^2　は、即ち、　ｘ≧０ において、　３ｙ＝±√ｘ｜ｘ−３｜　である。

そこで、（１）は、曲線　ｙ＝（１/３）√ｘ（３−ｘ）　（０≦ｘ≦３）　の長さを求め、２倍すればよい。

　ここで、ｙ’＝（１−ｘ）/（２√ｘ）　なので、　１＋（ｙ’）²＝（ｘ＋１）²/（４ｘ）　なので、

　Ｌ＝２∫₀³ √（１＋（ｙ’）²）ｄｘ＝∫₀³ （√ｘ＋１/√ｘ）ｄｘ＝４

（２）は、よおすけさんのヒントを用いて、y=(1/3)t(t^2-3) の式の両辺を２乗すると、

　y^2=(1/9)(t^2)(t^2-3)^2 で、t^2=x　より整えると、9y^2=x(x-3)^2　となります。

　グラフは、下図のようになります。



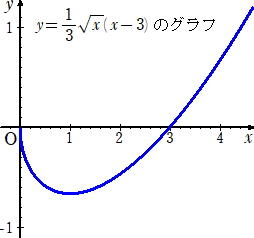
　よって、x軸によって切りとられる部分の長さは、（１）の半分で、２　となる。

＃　ＧＡＩさんの計算と一致して、安心しました．．．。