
問題 面積が12の四角形ABCDにおいて、AD=CDのとき、Dから辺BCに下した垂線DE
の長さを求めよ。
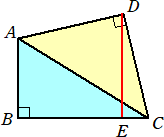
(答) △DECを切り取り、辺CDを辺ADに重ねることにより、1辺の長さがDEの正方形が作
れるので、DE2=12より、 DE=2
GAI さんからのコメントです。(令和元年8月7日付け)
もし、このアクロバティック解法を思いつかないならを想定して試みた。
図の4角形を、Dを原点に、Aをx軸上、Cをy軸上にとり、DA=DC=a、∠ADB=θ とすると、
∠ADC=∠ABC=90°から四角形ABCDはACを直径とする同一円周上にあり、
∠CAD=∠ACD=∠ABD=∠CBD=∠BDE=45°(DBは角Bの二等分線になっている。)
∠ADE=∠xAB=θ+45°から、DE//AB
求める長さ DE=x とおくと、BE=x、BD=√2*x、∠CDE=45°-θ で、
面積条件から、 △ABD+△BDE+△CDE=12
1/2*√2*x*a+1/2*x^2+1/2*x*a*sin(45°-θ)=12
x^2+√2/2*x*a*(sinθ+cosθ)=24
x^2+√2/2*x*a*√2*cos(45°-θ)=24
ここで、△CDEで、a*cos(45°-θ)=x であるので、上式は、x^2+x^2=24
∴x^2=12 より、x=DE=2*√3
如何にアイデアが大切かを教えてくれる。
らすかるさんからのコメントです。(令和元年8月7日付け)
もし、このアクロバティック解法を思いつかないなら...
DE=x、CE=a とおく。AからDEに垂線AHを下ろすと、△CDE≡△DAH なので、
AH=DE=x、DH=CE=a
よって、AB=HE=DE-DH=x-a なので、四角形ABCDの面積は、
(台形ABED+△CDE)=(AB+DE)AH/2+CE・DE/2=(2x-a)・x/2+ax/2=x^2=12
よって、x=2√3