擖弌椡亖侽丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
丂摉俫俹偑偄偮傕偍悽榖偵側偭偰偄傞俫俶乽俲丏俽丏乿偝傫偐傜偺弌戣偱偡丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂乮暯惉俀俆擭侾侾寧侾俉擔晅偗乯
丂乽擖弌椡亖侽乿偲偄偆栤戣傪峫偊傑偡丅侾乣値 傑偱偺悢傪巊偭偰丄僒僀僋儕僢僋側恾宍偵杽傔
偰偄偔栤戣偱偡丅
丂娙扨側椺偲偟偰丄乮奺捀揰偺擖弌偺悢偺榓偑侽偵側傞乯
丂丂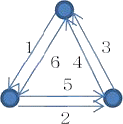 丂丂丂丂丂丂
丂丂丂丂丂丂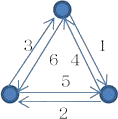
丂摨偠偔丄侾乣俇偱偡偑丄扨慄偺恾乮巐柺懱乯
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂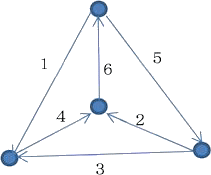
侾乣俉偺応崌偲丄侾乣侾侽偺応崌偺堦偮偲偟偰
丂丂丂丂丂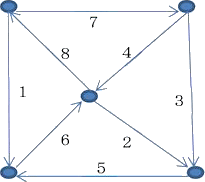 丂丂丂丂丂
丂丂丂丂丂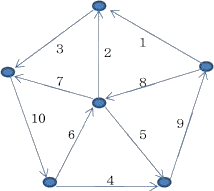
侾乣侾俀偺応崌丄丂椺丂俀捠傝
丂丂丂丂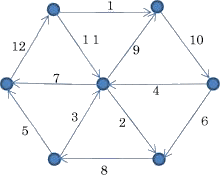 丂丂丂丂丂
丂丂丂丂丂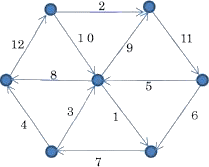
亙媈栤亜
乮侾乯暋悢偺夝偑丄偁傞応崌丄杮幙揑偵,婔捠傝偁傞偐丠
乮俀乯栴報偺岦偒偑丄堎側傞応崌傕壜擻偐丠
乮俁乯懠偺惓懡柺懱偺応崌偼丄壜擻偐丠
乮係乯拞偺悢偼丄係丆侾侽丆侾係丆侾俉偼丄昁慠偐丠
乮俆乯堦斒揑側夝朄偼偁傞偺偐丠
丂丂丂丂丂丂丂丂侾乣俋偺応崌丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂侾乣侾侾偺応崌
丂丂丂丂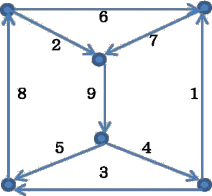 丂丂丂丂丂丂
丂丂丂丂丂丂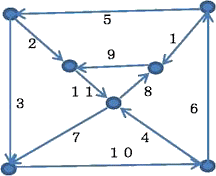
亙暘偐偭偨偙偲亜
丂昁梫忦審偵側傞偐傕抦傟傑偣傫偑丄奺捀揰偺擖傞栴報偑懡偔丄弌傞栴報偑彮側偄揰傪亄揰丄
媡傪亅揰丄摍偟偄偲偒侽揰偲偡傞偲丄慡懱偲偟偰丄亄揰偺屄悢偲亅揰偺屄悢偼堦抳偡傞丅
丂栴報偺岦偒傪慡偰媡偵偟偰傕惉傝棫偮丅
乮捛婰乯丂暯惉俀俆擭侾侾寧俀俋擔晅偗
丂惓榋柺懱偺応崌乮侾乣侾俀傑偱乯
丂敧屄偺捀揰偺抣亖侽乮亄A丄亅A乯偺僾儔僗晹暘乮擖乯偺憤榓偼丄侾乣侾俀傑偱偺憤寁俈俉偵摍
偟偄丅侾杮栴報偺擖弌偵拲栚偡傞偲丄椬偳偆偟偼摨偠抣偱側偗傟偽側傜側偄偺偱丄係杮偺悢偺
榓偑俁俋偵側傜側偗傟偽側傜側偄丅
丂傛偭偰丄係偮偺悢偺榓偑俁俋偵側傞(8,9,10,12),(7,9,11,12),(6,10,11,12)偺偆偪夝傪傕偮偺偼丄堦
偮偱乮7,9,11,12乯偺偲偒偩偗偱偁傝丄12偼堦杮偺擖椡偱丄埲壓偺擇偮偺夝偑偁傝丄栴報傪媡岦
偒偵曄偊傞偲丄偙偺栴報偺恾偱偼丄憤寁係捠傝乮夞揮丄斀揮傪彍偔乯偺夝偑懚嵼偡傞丅
丂丂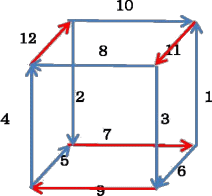 丂丂丂丂
丂丂丂丂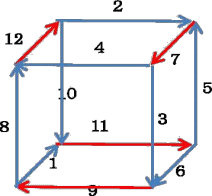
丂忋婰偺栤戣偵偮偄偰丄摉俫俹偑偄偮傕偍悽榖偵側偭偰偄傞俫俶乽峌棯朄乿偝傫偑峫嶡偝傟傑偟
偨丅乮暯惉俀俆擭侾俀寧俇擔晅偗乯
亙忬嫷徹嫆偲壖愢亜丂曈乮巬乯偺悢偵偮偄偰丄
丂丒慡懱偱偼丄値杮
丂丒1偮偺曈偵懳偟偰丄擖弌椡偁傢偣偰3杮埲忋偱偁傞丅劅仜 傗 劅仜劅丄亖仜 偼懚嵼偟側偄丅
丂捀揰乮愡乯偺抣乮擖椡懁傑偨偼弌椡懁偺榓乯
丂丒抣偺斖埻
丂丂亖仜劅側傜丄嵟彫丗1+2=3丄嵟戝丗値
丂丂亖仜亖側傜丄嵟彫丗1+4=2+3=5丄嵟戝丗n+(n-3)=(n-1)+(n-2)=2n-3
丂丂佭仜劅側傜丄嵟彫丗1+2+3=6丄嵟戝丗値丂丂丂丂側偳丒丒丒丅
丂丒慡懱偺榓偼丄儼k=1乣n k=n(n+1)/2丂乮埲壓丄儼偲婰偡乯偱偁傞丅
丂採帵偝傟偨傕偺傛傝丄
| 丂 |
丂丂n=6偺応崌丄儼=21 |
丂 |
丂丂n=9偺応崌丄儼=45 |
|
丂丂丂丂丂嘐
丂丂丂丂乛嘐乢
丂丂丂嘋劅劅劅嘍 |
|
丂丂丂嘒劅嘐
丂丂丂劆嘓劆
丂丂丂劆嘓劆
丂丂丂嘒劅嘍 |
丂曈乮巬乯偲捀揰乮愡乯偺抣丗暘妱悢偲側傞丅
丂恾宍傪屌掕偟偰峫偊偰丄悢偊忋偘偰傒傞丅
仠丂k妏悕偺偲偒
丂値偑拰偵偁傞応崌丄1亝a 偐偮 2a亙n=2k 偲偡傞丅
丂丂仜
丂
n伀丂丂乧丂劆丂丂乧丂劆
丂仼仜仺丂丂丂仜劅丂丂丂仜仼
丂a丂 n-a丂丂丂丂丂丂丂丂
a
丂値偑掙柺偵偁傞応崌丄1亝a亙b亙n=2k 偲偡傞丅
丂丂 仜
丂n-a伀 b仾丂丂乧丂劆丂丂乧丂劆
丂
仺仜仺仜仺丂丂丂仜劅丂丂丂仜仺
丂丂a丂n丂n-b丂丂丂丂丂丂丂丂丂a |
丂 |
丂丂 仜
丂n-a伀n-b仾丂丂乧丂劆丂丂乧丂劆
丂
仺仜仺 仜仺丂丂丂仜劅丂丂丂仜仺
丂丂a丂n丂丂b丂丂丂丂丂丂丂丂丂 a |
| 丂 |
|
|
丂丂 仜
丂丂a伀 b仾丂丂乧丂劆丂丂乧丂劆
丂
仺仜仺仜仺丂丂丂仜劅丂丂丂仜仺
丂n-a丂n丂n-b丂丂丂丂丂丂丂丂丂n-a |
|
丂丂 仜
丂丂a伀n-b仾丂丂乧丂劆丂丂乧丂劆
丂
仺仜仺 仜仺丂丂丂仜劅丂丂丂仜仺
丂n-a丂n丂丂b丂丂丂丂丂丂丂丂丂
n-a |
偺傛偆偵丄偼偟偛忬偵揥奐偡傞丅
丂3妏悕乮惓4柺懱乯偺応崌丂丂n=6偺偲偒
丂丂嘐
丂 6伀
2仾 4仾
丂仼嘐仺嘍仺嘋仼
丂 1丂 5丂 3丂 1
丂3妏悕宯偺暯柺恾宍
丂丂丂丂丂丂嘐
丂丂丂丂 乛6仾
乢
丂丂 1 乛丂 嘐丂 乢 5
丂丂丂伀 4乛丂乢2
伀
丂丂丂嘋仼劅劅劅劅嘍
丂丂丂丂丂丂3 |
丂 |
丂丂丂丂丂嘋
丂丂丂 1乛仾乢4
丂丂劇嘐 3劆丂嘐劉
丂丂劆 5乢劆乛2
劆
丂丂劆丂丂嘍丂丂劆
丂丂劋劅 仼 劅劊
丂丂丂丂丂6 |
丂4妏悕偺応崌丂丂n=8偺偲偒
丂丂嘔
丂
8伀 4仾 2伀 6仾
丂仼嘒仺嘑仺嘍仺嘐仼
丂 1丂 7丂 3丂 5丂 1 |
丂 |
丂丂嘕
丂 8伀 5仾 6仾
3伀
丂仼嘒仺嘑仺嘐仼嘋仼
丂 1丂 7丂 2丂 4丂 1 |
丂 |
丂丂嘓
丂 8伀 1伀 4仾
5仾
丂仼嘒仺嘑仺嘑仺嘍仼
丂 2丂 6丂 7丂 3丂 2 |
| 丂 |
|
|
|
|
丂丂嘖
丂 8伀 7仾 4伀
5仾
丂仼嘒仺嘑仼嘋仺嘍仼
丂 2丂 6丂 1丂 3丂 2 |
|
丂丂嘕
丂 8伀 7仾 4仾
3伀
丂仼嘒仺嘑仼嘍仼嘍仼
丂 2丂 6丂 1丂 5丂 2 |
|
丂丂嘓
丂 8伀 1伀 2仾
7仾
丂仼嘒仺嘐仺嘐仺嘑仼
丂 3丂 5丂 6丂 4丂 3 |
| 丂 |
|
|
|
|
丂丂嘔
丂 8伀 2伀 6仾
4仾
丂仼嘒仺嘑仺嘑仺嘋仼
丂 3丂 5丂 7丂 1丂 3 |
|
丂丂嘔
丂 7伀 6仾 3伀
4仾
丂仺嘒仺嘒仺嘍仺嘍仺
丂 1丂 8丂 2丂 5丂 1 |
|
丂丂嘕
丂 7伀 6仾 5仾
4伀
丂仺嘒仺嘒仺嘍仼嘋仺
丂 1丂 8丂 2丂 3丂 1 |
| 丂 |
|
|
|
|
丂丂嘐
丂 2伀 5仾 4伀
1仾
丂仺嘒仺嘒仺嘑仺嘑仺
丂 6丂 8丂 3丂 7丂 6 |
|
丂丂嘓
丂 2伀 5仾 4仾
7伀
丂仺嘒仺嘒仺嘋仼嘑仺
丂 6丂 8丂 3丂 1丂
6 |
|
|
仠 k妏拰偺偲偒丂丂1亝a亙b亙n=3k 偲偡傞丅
丂値偑拰偵偁傞応崌
丂a丂 n-a丂丂丂丂丂丂丂丂
a
丂仺仜仼丂丂丂仜劅丂丂丂仜仺
丂 n伀丂丂乧丂劆丂丂乧丂劆
丂仼仜仺丂丂丂仜劅丂丂丂仜仼
丂b丂 n-b丂丂丂丂丂丂丂丂
b |
丂 |
丂a丂 n-a丂丂丂丂丂丂丂丂 a
丂仺仜仼丂丂丂仜劅丂丂丂仜仺
丂
n伀丂丂乧丂劆丂丂乧丂劆
丂仼仜仺丂丂丂仜劅丂丂丂仜仼
丂n-b丂
b丂丂丂丂丂丂丂丂n-b |
丂値偑忋柺乮傑偨偼掙柺乯偵偁傞応崌
丂 a丂 n丂丂b丂丂丂丂丂丂丂丂丂 a
丂 仺仜仺
仜仺丂丂丂仜劅丂丂丂仜仺
丂n-a仾n-b伀丂丂乧丂劆丂丂乧丂劆
丂 劅仜劅 仜劅丂丂丂仜劅丂丂丂仜劅 |
丂 |
丂 a丂
n丂丂n-b丂丂丂丂丂丂丂丂 a
丂 仺仜仺 仜仺丂丂丂仜劅丂丂丂仜仺
丂n-a仾丂b伀丂丂乧丂劆丂丂乧丂劆
丂 劅仜劅
仜劅丂丂丂仜劅丂丂丂仜劅 |
| 丂 |
|
|
丂n-a丂 n丂丂b丂丂丂丂丂丂丂丂丂n-a
丂 仺仜仺
仜仺丂丂丂仜劅丂丂丂仜仺
丂丂a仾n-b伀丂丂乧丂劆丂丂乧丂劆
丂 劅仜劅 仜劅丂丂丂仜劅丂丂丂仜劅
|
|
丂n-a丂
n丂丂n-b丂丂丂丂丂丂丂丂n-a
丂 仺仜仺 仜仺丂丂丂仜劅丂丂丂仜仺
丂丂a仾丂b伀丂丂乧丂劆丂丂乧丂劆
丂 劅仜劅
仜劅丂丂丂仜劅丂丂丂仜劅 |
偺傛偆偵丄偼偟偛忬偵揥奐偡傞丅
丂3妏拰偺応崌丂丂n=9偺偲偒
丂 1丂 8丂
5丂 1 丂丂 1丂 8丂 6丂 1丂丂丂 2丂 7丂 6丂 2
丂仺嘓仼嘒仼嘐仺丂丂丂仺嘓仼嘒仼嘑仺丂丂丂仺嘓仼嘑仼嘒仺
丂 9伀 3仾
6仾丂丂丂丂 9伀 2仾 7仾丂丂丂丂 9伀 1仾 8仾
丂仼嘓仺嘑仺嘐仼丂丂丂仼嘓仺嘍仺嘑仼丂丂丂仼嘓仺嘋仺嘒仼
丂 2丂 7丂 4丂 2 丂丂
4丂 5丂 3丂 4 丂丂丂 5丂 4丂 3丂 5
丂 8丂 9丂 6丂 8 丂丂 2丂 9丂 6丂 2 丂丂 3丂 9丂 4丂
3
丂仺嘓仺嘓仺嘒仺丂丂丂仺嘓仺嘓仺嘐仺丂丂丂仺嘓仺嘓仺嘋仺
丂 1仾 3伀 2仾丂丂丂丂 7仾 3伀 4伀丂丂丂丂 6仾 5伀
1伀
丂仺嘍仺嘑仺嘑仺丂丂丂仼嘒仼嘒仼嘍仼丂丂丂仺嘒仺嘑仺嘒仺
丂 5丂 4丂 7丂 5 丂丂 1丂 8丂 5丂 1 丂丂 8丂 2丂 7丂
8
丂3妏拰宯偺暯柺恾宍
丂丂丂丂丂丂嘋
丂丂丂丂丂乛伀1乢
丂丂丂丂乛丂嘑 丂乢
丂丂 3乛丂6乛乢7
丂乢4
丂丂乛 丂嘒劅仺嘓 丂乢
丂丂伀8乛丂 2丂丂乢9
仾
丂丂嘒仼劅劅劅劅劅劅嘓
丂丂丂丂丂丂5 |
丂 |
丂丂丂丂6
丂丂嘒劅劅仺嘑
丂丂仾2乢乛7仾
丂丂劆丂嘓丂劆
丂
8劆
9伀丂劆1
丂丂劆丂嘓丂劆
丂丂劆5乛乢4劆
丂丂嘒仼劅劅嘋
丂丂丂丂3 |
丂4妏拰偺応崌乮惓6柺懱乯
丂
1丂11丂 5丂 8丂 1
丂仺嘖仼嘕仼嘒仼嘓仺
丂12伀 6仾 3伀 9仾
丂仼嘖仺嘔仺嘑仺嘓仼
丂 2丂10丂 4丂 7丂
2 |
丂 |
丂 1丂11丂 4丂 6丂 1
丂仺嘖仼嘕仼嘔仺嘐仺
丂12伀 7仾10仾 5伀
丂仼嘖仺嘓仺嘔仼嘒仼
丂 3丂 9丂
2丂 8丂 3 |
丂 |
丂 2丂10丂11丂 5丂 2
丂仺嘖仼嘕仼嘕仼嘑仺
丂12伀 1伀 6仾 7仾
丂仼嘖仺嘓仺嘓仺嘑仼
丂
4丂 8丂 9丂 3丂 4 |
| 丂 |
|
|
|
|
丂 2丂10丂 1丂 7丂 2
丂仺嘖仼嘕仺嘑仺嘑仺
丂12伀11仾 6仾
5伀
丂仼嘖仺嘕仼嘓仼嘓仼
丂 4丂 8丂 3丂 9丂 4 |
|
丂 3丂 9丂10丂 8丂 3
丂仺嘖仼嘔仼嘔仼嘕仺
丂12伀
1伀 2仾11仾
丂仼嘖仺嘐仺嘐仺嘕仼
丂 7丂 5丂 6丂 4丂 7 |
|
丂 4丂 8丂11丂 2丂
4
丂仺嘖仼嘕仼嘕仼嘐仺
丂12伀 3伀 9仾 6仾
丂仼嘖仺嘔仺嘔仺嘐仼
丂 5丂 7丂10丂 1丂
5 |
乮捛婰乯丂暯惉俀俆擭侾俀寧俈擔晅偗
仠丂惓k妏宍偺偲偒丂丂摍嵎悢楍偺惈幙傪棙梡偟偰丄惓懡妏宍偺曈忋偵悢帤傪攝抲偡傞丅
n=2k偺偲偒
偦偺侾
丂丂1丂 2丂 3丂
4丂丂丂 k丂 1
丂丂仺仜仺仜仺仜仺仜 乧 仺仜仺
丂丂仼丂仼丂仼丂仼丂丂丂仼丂仼
丂丂k+1 k+2 k+3 k+4丂丂
2k丂k+1
| 椺 |
丂丂1丂 2丂 1
丂丂仺嘍仺嘍仺
丂丂仼丂仼丂仼
丂丂3丂 4丂 3
丂偡側傢偪丄
丂丂
2,3
丂丂嘍仺嘍
丂丂丂仼
丂丂 1,4 |
丂 |
丂丂1丂 2丂 3丂
1
丂丂仺嘐仺嘒仺嘑仺
丂丂仼丂仼丂仼丂仼
丂丂4丂 5丂 6丂 4
丂偡側傢偪丄
丂丂丂丂丂嘐
丂丂 1,4//
乢乢2,5
丂丂丂 嘑 亖 嘒
丂丂丂丂丂3,6 |
丂 |
丂丂1丂 2丂 3丂 4丂
1
丂丂仺嘑仺嘓仺嘕仺嘓仺
丂丂仼丂仼丂仼丂仼丂仼
丂丂5丂 6丂 7丂 8丂 5
丂偡側傢偪丄
丂丂丂丂2,6
丂丂丂
嘑亖嘓
丂丂1,5||丂||3,7
丂丂丂 嘓亖嘕
丂丂丂丂 4,8 |
偦偺俀
丂 1丂 2丂 3丂 4丂丂丂丂k丂
1
丂丂佀仜佀仜佀仜佀仜 乧 佀仜佀
丂 2k 2k-1 2k-2 2k-3丂丂k+1
2k
丂儼偑k偱妱傝愗傟傞偺偱丄捀揰偺抣乮=2k+1乯偑偡傋偰摨偠偲側傞丅
| 椺 |
丂丂1丂 2丂
1
丂丂佀嘍佀嘍佀
丂丂4丂 3丂 4
丂偡側傢偪丄
丂丂 1,4
丂丂嘍仺嘍
丂丂丂仼
丂丂
2,3 |
丂 |
丂丂1丂 2丂 3丂 1
丂丂佀嘑佀嘑佀嘑佀
丂丂6丂 5丂 4丂
6
丂偡側傢偪丄
丂丂丂丂丂嘑
丂丂 1,6// 乢乢2,5
丂丂丂 嘑 亖 嘑
丂丂丂丂丂3,4 |
丂 |
丂丂1丂
2丂 3丂 4丂 1
丂丂佀嘓佀嘓佀嘓佀嘓佀
丂丂8丂 7丂 6丂 5丂 8
丂偡側傢偪丄
丂丂丂丂2,7
丂丂丂
嘓亖嘓
丂丂1,8||丂||3,6
丂丂丂 嘓亖嘓
丂丂丂丂
4,5 |
n=2k+1偺偲偒
丂2k+1丂1丂 2丂 3丂丂丂k丂2k+1
丂丂仺仜佀仜佀仜佀仜 乧
佀仜仺
丂丂丂丂2k 2k-1 2k-2丂
k+1
丂儼偑(k+1)偱妱傝愗傟傞偺偱丄捀揰偺抣乮=2k+1乯偑偡傋偰摨偠偲側傞丅
| 椺 |
丂3丂 1
3
丂仺嘊佀嘊仺
丂丂丂2
丂偡側傢偪丄
丂丂1,2
丂嘊佭嘊
丂丂3 |
丂 |
丂5丂 1丂 2
5
丂仺嘍佀嘍佀嘍仺
丂丂丂4丂 3
丂偡側傢偪丄
丂丂丂丂丂嘍
丂丂 1,4// 乢5
丂丂丂 嘍 亖
嘍
丂丂丂丂丂2,3 |
丂 |
丂7丂 1丂 2丂 3 7
丂仺嘑佀嘑佀嘑佀嘑仺
丂丂丂6丂 5丂
4
丂偡側傢偪丄
丂丂丂丂2,5
丂丂丂 嘑亖嘑
丂丂1,6||丂||3,4
丂丂丂 嘑劅嘑
丂丂丂丂 7 |
丂俲丏俽丏偝傫偐傜偺僐儊儞僩偱偡丅乮暯惉俀俆擭侾俀寧俈擔晅偗乯
丂惓榋柺懱偱怴偨側夝偑尒偮偐傝丄峌棯朄偝傫偵丄姶幱偱偡丅傑偟偨丅 廳暋偡傞晹暘偲偦偆
偱側偄晹暘偑偁傝丄憤寁侾係捠傝丄偦傟埲忋偁傞偺偐傑偩傢偐傝 傑偣傫丅 惓敧柺懱偵偮偄
偰丄俉捠傝尒偮偐傝傑偟偨偑丄偦傟埲忋偁傞偐傕偟傟傑偣傫丅
丂惓敧柺懱偺応崌乮侾乣侾俀乯
丂丂丂丂丂丂丂丂丂丂丂丂丂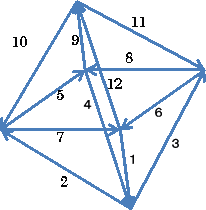
丂偙偺恾偺応崌丄懳徧側宍偱偁傝丄偳偺摨堦暯柺忋偺係杮偺榓傕丄俀俇偱側偗傟偽側傜側偄偙
偲偑傢偐傝丄偳偺堦慻傕係悢偺榓偑俀俇偵側傞応崌偑慡晹偱俆捠傝偁傝傑偡丅
丂乮俙乯丂(5,6,7,8),(2,3,10,11),(1,4,9,12)丂丂丂乮俛乯丂(4,6,7,9),(2,5,8,11),(1,3,10,12)
丂乮俠乯丂(4,5,8,9),(3,6,7,10),(1,2,11,12)丂丂丂乮俢乯丂(3,5,8,10),(2,4,9,11),(1,6,7,12)
丂乮俤乯丂(3,4,9,10),(2,6,7,11),(1,5,812)
丂偙偺拞偱丄乮俤乯埲奜偼壜擻偱丄媡岦偒傕娷傔俉捠傝偁傝傑偡丅寢壥偳偺応崌傕岦偐偄崌偆捀
揰偺抣偺榓偑俀俇偵側偭偰偄傞丅偙傟偑堦斒偺懠偺恾偺応崌傕昁梫忦審偵側偭偰偄傞偱偟傚
偆偐丠

 丂丂丂丂丂丂
丂丂丂丂丂丂

 丂丂丂丂丂
丂丂丂丂丂
 丂丂丂丂丂
丂丂丂丂丂
 丂丂丂丂丂丂
丂丂丂丂丂丂
 丂丂丂丂
丂丂丂丂
