当ＨＰがいつもお世話になっているＨＮ「よおすけ」さんからの出題です。
（令和３年９月１日付け）
次の（選択問題A）、（選択問題B）のうち、どちらか一題を選んで答えよ。
(選択問題A)
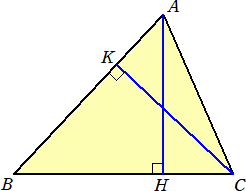
∠Bが鋭角である△ABCにおいて、頂点Aから辺BCまたはその延長上に垂線を引き交点
をHとし、また頂点Cから辺ABまたはその延長上に垂線を引き交点をKとする。
2BH/BC、2BK/BAが整数であるとき、次の問に答えよ。
(1) cosBの値は、1/2、1/
、
/2のいずれかでなければならないことを示せ。(2) 上にあげたcosBのおのおのの値に対して、条件を満たす3角形があれば、その例を
1つずつあげよ。
(選択問題B)
∠Bが鋭角である△ABCにおいて、頂点Aから辺BCまたはその延長上に垂線を引き交点
をHとし、また頂点Cから辺ABまたはその延長上に垂線を引き交点をKとする。
2BH/BC、2BK/BAが整数であるとき、△ABCはどのような3角形であるか。
（出典） 選択問題A：大阪大学前期文系（1976）
選択問題B： 大阪大学前期理系（1976）
（答） ＨＮ「高校三年生」さんからのコメントです。（令和３年９月２日付け）
「正三角形」か「直角二等辺三角形」か「頂角が120°の二等辺三角形」では？
（コメント） ４５年前の問題に敬意を表しつつ、挑戦してみました。
ｃｏｓＢ＝ＢＨ/ＢＡ＝ＢＫ/ＢＣ より、
２ＢＡｃｏｓＢ/ＢＣ＝２ＢＨ/ＢＣ 、２ＢＣｃｏｓＢ/ＢＡ＝２ＢＫ/ＢＡ
はともに整数なので、 ２ＢＡｃｏｓＢ/ＢＣ×２ＢＣｃｏｓＢ/ＢＡ＝４ｃｏｓ2Ｂ は整数
０＜Ｂ＜９０°なので、 ０＜ｃｏｓＢ＜１
このことから、 ４ｃｏｓ2Ｂ＝１、２、３ 即ち、 ｃｏｓＢ＝１/２、１/
、/２ である。（イ） ｃｏｓＢ＝１/２ 即ち、Ｂ＝６０°のとき、ＢＨ/ＢＡ＝ＢＫ/ＢＣ＝１/２ より、
ＢＡ＝２ＢＨ 、ＢＣ＝２ＢＫ である。
このとき、 ２ＢＨ/ＢＣ＝ＢＡ/ＢＣ 、２ＢＫ/ＢＡ＝ＢＣ/ＢＡ が共に整数なので、
ＢＡ/ＢＣ＝１ 即ち、 ＢＡ＝ＢＣ から、△ＡＢＣは２等辺三角形で、
Ｂ＝６０°より、△ＡＢＣは正三角形である。
（ロ） ｃｏｓＢ＝１/
即ち、Ｂ＝４５°のとき、ＢＨ/ＢＡ＝ＢＫ/ＢＣ＝１/ より、ＢＡ＝
ＢＨ 、ＢＣ＝ＢＫ である。このとき、２ＢＨ/ＢＣ＝
ＢＡ/ＢＣ 、２ＢＫ/ＢＡ＝ＢＣ/ＢＡ が共に整数なので、ＢＡ/ＢＣ＝ｍ 、ＢＣ/ＢＡ＝ｎ （ｍ、ｎは整数）とおける。辺々かけて、 ｍｎ＝２ から、 （ｍ，ｎ）＝（２，１）、（１，２）
（ｍ，ｎ）＝（２，１）のとき、 ＢＡ＝
ＢＣ で、∠ＡＣＢ＝９０°となる。よって、△ＡＢＣは、Ｃ＝９０°の直角２等辺三角形である。
（ｍ，ｎ）＝（１，２）のときも同様で、△ＡＢＣは、Ａ＝９０°の直角２等辺三角形である。
（ハ） ｃｏｓＢ＝
/２ 即ち、Ｂ＝３０°のとき、ＢＨ/ＢＡ＝ＢＫ/ＢＣ＝/２ より、ＢＨ＝（
/２）ＢＡ 、ＢＫ＝（/２）ＢＣ である。このとき、２ＢＨ/ＢＣ＝
ＢＡ/ＢＣ 、２ＢＫ/ＢＡ＝ＢＣ/ＢＡ が共に整数なので、ＢＡ/ＢＣ＝ｍ 、ＢＣ/ＢＡ＝ｎ （ｍ、ｎは整数）とおける。辺々かけて、 ｍｎ＝３ から、 （ｍ，ｎ）＝（３，１）、（１，３）
（ｍ，ｎ）＝（３，１）のとき、 ＢＡ＝
ＢＣ で、ＡＣ2＝ＢＣ2＋ＢＡ2−２・ＢＣ・ＢＡｃｏｓ３０°
＝ＢＣ2＋３ＢＣ2−２・ＢＣ・
ＢＣ・（/２）＝ＢＣ2 より、 ＡＣ＝ＢＣよって、△ＡＢＣは、Ａ＝Ｂ＝３０°、Ｃ＝１２０°の２等辺三角形である。
（ｍ，ｎ）＝（１，３）のとき、 ＢＣ＝
ＢＡ で、ＡＣ2＝ＢＣ2＋ＢＡ2−２・ＢＣ・ＢＡｃｏｓ３０°
＝３ＢＡ2＋ＢＡ2−２・
ＢＡ・ＢＡ・（/２）＝ＢＡ2 より、 ＡＣ＝ＢＡよって、△ＡＢＣは、Ｂ＝Ｃ＝３０°、Ａ＝１２０°の２等辺三角形である。
（コメント） これで合っているかな？よく練れた問題ですね！
当ＨＰがいつもお世話になっているＰＢさんからのコメントです。（令和３年９月２日付け）
ご無沙汰しております。上記の問題で、図形的な解を考えました。∠Ａが鈍角のときは、
ちょっと苦しい感じですが…。
任意の三角形において、２つの角は鋭角なので、∠Ｃも鋭角として一般を失わない。
このとき、Ｈは辺ＢＣ上にあり、ＢＨ＜ＢＣ で、０＜２ＢＨ/ＢＣ＜２ＢＣ/ＢＣ＝２ より、
２ＢＨ/ＢＣ が整数となるのは、２ＢＨ/ＢＣ＝１ に限られる。
ＢＣ＝２ＢＨ より、ＨはＢＣの中点となる。ＡＨがＢＣの垂直二等分線であることから、
△ＡＢＣはＡＢ＝ＢＣの二等辺三角形である。
以下、∠Ａによって場合分けする。
１．∠Ａが鋭角のとき、
Ｋは辺ＡＢ上にあり、上記とまったく同様にして、ＢＣ＝ＡＣ なので、△ＡＢＣは正三角形
２．∠Ａが直角のとき、
ＡとＫは一致するので、２ＢＡ/ＢＫ＝２ となり、条件をみたす。
このとき、ＡＢ＝ＡＣ、∠Ａ＝９０°の直角二等辺三角形
３．∠Ａが鈍角のとき、
ＢＡ＜ＢＫ である。また、△ＡＢＣにおいて、ＢＡ＋ＣＡ＝２ＢＡ＞ＢＣ
直角三角形ＢＣＫにおいて、斜辺ＢＣは最大辺であるから、ＢＫ＜ＢＣ
よって、ＢＡ＜ＢＫ＜２ＢＡ から、２＜２ＢＫ/ＢＡ＜４ で、２ＢＫ/ＢＡ が整数となるのは、
２ＢＫ/ＢＡ＝３ に限られ、２ＢＫ＝３ＢＡ から、ＡはＢＫを２：１に内分している。
いま、線分ＢＫに関して点Ｃと対称な点をＤとすれば、Ｄ、Ｋ、Ｃは同一直線上にあり、
点Ａは，△ＤＢＣの重心かつ外心なので、△ＤＢＣは正三角形であり、ＢＡはその対称軸
以上により、△ＡＢＣは、∠Ｂ＝∠Ｃ＝３０°の二等辺三角形
（コメント） ＰＢさん、いつもご投稿、ありがとうございます。特に、３．の証明は圧巻ですね！
ただ、∠Ｃが鈍角の場合もありえるので、別途証明が必要かな？と思いました。