当ＨＰがいつもお世話になっているＨＮ「よおすけ」さんからの出題です。
（令和３年４月１日付け）
AB＝−１＋
、CA＝２、∠C＝π/１２ である三角形を解け。（答） スモークマンさんが考察されました。（令和３年４月１日付け）
気づけました♪
１辺が２の正三角形ACDをAから垂線を引いて、CDとの交点をHとする。Hから１上がった
点をBとすれば、AB＝
−１、∠C＝６０°−４５°＝１５°なる△ABCが出来上がりますね ^^まだあったのでした...^^;; 畏友 たけちゃんさんからのものです ^^。
スモークマンさんの言われる図のケースもありますが、三角形ABB’が AB＝AB’ の直角
二等辺三角形になるように△ABCの外側にB’をとるとき、B’の位置がB点であることにす
ると、別の三角形も作れます。つまり、この設定では、△ABCの形状は１つに定まりません。
以下のようにするのが普通でしょうか。
AB＝
−１、∠C＝π/１２、CA＝２ より、(−１)/sin(π/１２)＝２/sin∠B となって、sin(π/１２)＝(
−
)/４ より、２＝２/sin∠B すなわち、sin∠B＝１/ だから、∠B＝π/４ または ３/４
よって、
「∠B＝π/４、∠A＝２π/３、BC＝
」 または 「∠B＝３π/４、∠A＝π/６、BC＝」となると思います。
よおすけさんからのコメントです。（令和６年８月１０日付け）
この問題の三角形を、下図のように表してみました。
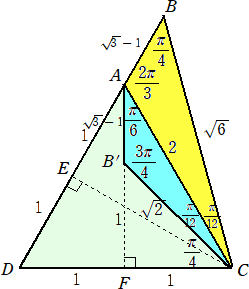
(補足) 黄色または水色部分の三角形が求める三角形
辺の長さ： ＡＤ＝ＤＣ＝ＣＡ＝２ 、ＢＥ＝ＥＣ＝ＡＦ＝
、ＢＣ＝ 、Ｂ’Ｃ＝ＡＢ＝ＡＢ’＝−１＋
、Ｂ’Ｆ＝ＦＣ＝１以下、工事中！