三角形の個数　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　　

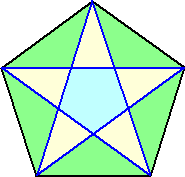
左図において、三角形は何個あるか？

（答）　地道に数えると、　１０＋１５＋５＋５＝３５（個）


（コメント）　計算式一発で求めることは可能だろうか？


　らすかるさんからのコメントです。（令和元年７月７日付け）

　正ｎ角形の全対角線を引いて出来る三角形の個数は、「A006600」にありました。

　３本以上の対角線が１点で交わらなければ、

　　_nC₃＋_nC₄×4＋_nC₅×5＋_nC₆　（ただし、n＜r のとき、_nC_r＝0　とする）

で求められるようです。

　_nC₃ は、正ｎ角形の３頂点を選んで出来る三角形の個数

　_nC₄×4 は、正ｎ角形の２頂点と対角線の交点一つで出来る三角形の個数
（n頂点から4頂点A、B、C、Dを選んでACとBDの交点をOとすると、△OAB、△OBC、△OCD、
△ODAの4つの三角形が出来ます。）

　_nC₅×5 は、正ｎ角形の１頂点と対角線の交点二つで出来る三角形の個数
（n頂点から5頂点A、B、C、D、Eを選んでBDとCE、CEとDA、DAとEB、EBとAC、ACとBDの交
点を順にF、G、H、I、Jとすると、△AIH、△BJI、△CFJ、△DGF、△EHGの5つの三角形が出
来ます。）

　_nC₆ は、正ｎ角形の対角線の交点三つで出来る三角形の個数
（n頂点から6頂点A、B、C、D、E、Fを選ぶと、AD、BE、CFの3直線で三角形が出来ます。）

　従って、正五角形の場合は、　₅C₃＋₅C₄×4＋₅C₅×5＝35（個）　となります。

　正六角形ABCDEFの場合は、AD、BE、CFの3直線が1点で交わり、_nC₆で計算される三角
形が出来ませんので、

　　₆C₃＋₆C₄×4＋₆C₅×5＝110（個）　となります。

　正方形では、　₄C₃＋₄C₄×4＝8（個）、正三角形では、₃C₃＝1（個）　です。


（コメント）　地道な計算を裏付ける計算式に感動しました！らすかるさんに感謝します。


　ＧＡＩ さんからのコメントです。（令和元年７月１０日付け）

　正ｎ角形の全対角線を引いて出来る図形に対して、三角形の個数を探すのも面白いが、
「点の個数」、「線の個数」、「面の個数」も気になるテーマである。

　実際作図して数を見てみると、n=6位までは何とか数えられそうで、

   n=>    点の数：   線の数：   面の数
   1=>         1:        0:        0
   2=>         2:        1:        0
   3=>         3:        3:        1
   4=>         5:        8:        4
   5=>        10:       20:       11
   6=>        19:       42:       24

　これ以上を、図形を作図することから数えることは困難を伴い、nが10を越えればもう絶望
的になる。

　この先のそれぞれの数がどうなっていくかを知りたくて、「A006600」に貼られているリンク
先をいろいろ調べていたら、どうも次の様な手段と結果が出るようです。

　３つの数列を作り出すのに共通の関数 del(m,n) として、

　　del(m,n)=if(Mod(n,m)==0,1,0) 　#nをmが割り切れば1にそれ以外なら0を返す関数

を定義しておく。すると、正n角形の全対角線を引いて出来る図形Fnでの点の総数Point（n）
は、

Point(n)=if(n<4,0,binomial(n,4)+n
             -del(2,n)*(5*n^3-45*n^2+70*n-24)/24
             -del(4,n)*(3*n/2)
             -del(6,n)*n*(45*n-262)/6
             +del(12,n)*(42*n)
             +del(18,n)*(60*n)
             +del(24,n)*(35*n)
             -del(30,n)*(38*n)
             -del(42,n)*(82*n)
             -del(60,n)*(330*n)
             -del(84,n)*(144*n)
             -del(90,n)*(96*n)
             -del(120,n)*(144*n)
             -del(210,n)*(96*n))

　同じく線分の総数Line(n)は、

Line(n)=if(n<4,n*(n-1)/2,n*(n-1)*(n^2-5*n+12)/12
             -del(2,n)*n*(5*n^2-44*n+60)/16
             -del(4,n)*(9*n/4)
             -del(6,n)*n*(143*n-834)/12
             +del(12,n)*(133*n/2)
             +del(18,n)*(92*n)
             +del(24,n)*(54*n)
             -del(30,n)*(74*n)
             -del(42,n)*(132*n)
             -del(60,n)*(528*n)
             -del(84,n)*(222*n)
             -del(90,n)*(144*n)
             -del(120,n)*(222*n)
             -del(210,n)*(144*n))

　同じく面の総数Region(n)は、

Region(n)=if(n<3,0,(n-2)*(n-1)*(n^2-3*n+12)/24
             -del(2,n)*(n-2)*(5*n^2-32*n-24)/48
             -del(4,n)*(3*n/4)
             -del(6,n)*n*(53*n-310)/12
             +del(12,n)*(49*n/2)
             +del(18,n)*(32*n)
             +del(24,n)*(19*n)
             -del(30,n)*(36*n)
             -del(42,n)*(50*n)
             -del(60,n)*(198*n)
             -del(84,n)*(78*n)
             -del(90,n)*(48*n)
             -del(120,n)*(78*n)
             -del(210,n)*(48*n))

　これらを、n=1〜20で走らせると、

n=>     点の総数:  線の総数:    面の総数
1=>           1:         0:          0
2=>           2:         1:          0
3=>           3:         3:          1
4=>           5:         8:          4
5=>          10:        20:         11
6=>          19:        42:         24
7=>          42:        91:         50
8=>          57:       136:         80
9=>         135:       288:        154
10=>        171:       390:        220
11=>        341:       715:        375
12=>        313:       756:        444
13=>        728:      1508:        781
14=>        771:      1722:        952
15=>       1380:      2835:       1456
16=>       1393:      3088:       1696
17=>       2397:      4896:       2500
18=>       1855:      4320:       2466
19=>       3895:      7923:       4029
20=>       3861:      8360:       4500

　n=18では、減少していることが不思議で面白い。

　もちろん、n=100、1000、10000でもそれなりの値が計算できるのがすごいです。

　この３つが形式的に同じような（勿論それぞれには固有の式が微妙に違ってくるが･･･）も
ので導き出せることが興味を引く。

　言わずもがなオイラーは、点 - 線 + 面に不変量が潜んでいることを見通していたことを
やはり改めて感心します。