当ＨＰがいつもお世話になっているＨＮ「よおすけ」さんからの出題です。
（平成２４年３月２１日付け）
ｘ＝cosα＋i・sinα、y＝cosβ＋i・sinβ、z=cosγ＋i・sinγ が、ｘ＋ｙ＋ｚ＝ｘｙｚ であれば
cos(β−γ)＋cos(γ−α)＋cos(α−β)＝−１ であることを証明せよ。
（出典： モノグラフ 複素数(初版) より 問題14(その3)の6番）
（答） モノグラフには、「△ｘｙｚの３頂点および垂心が単位円の周上にあるので、この三角
形は直角三角形」というヒントが書いてあります。このヒントをどう使うかも思案のしど
ころですね！（モノグラフは私の高校時代の教科書だったので懐かしいです．．．(^^;)）
△ｘｙｚは、単位円に内接する三角形なので、ｘ＋ｙ＋ｚ は、△ｘｙｚの垂心である。
ｘ＋ｙ＋ｚ＝ｘｙｚ より、｜ｘ＋ｙ＋ｚ｜＝１ が成り立ち、垂心 ｘ＋ｙ＋ｚ も単位円周上の点で
ある。よって、△ｘｙｚは、直角三角形となる。
このとき、 ｘ＋ｙ＋ｚ＝ｘ または ｘ＋ｙ＋ｚ＝ｙ または ｘ＋ｙ＋ｚ＝ｚ
以下で、題意より、ｘ＋ｙ＋ｚ＝ｘ としても一般性は失われない。
このとき、 ｙ＋ｚ＝０ かつ ｙｚ＝１ から、 ｙ、ｚ は、２次方程式 ｔ2＋１＝０ の解。
ｔ＝±ｉ なので、 ｙ＝ｉ 、ｚ＝−ｉ としても一般性は失われない。
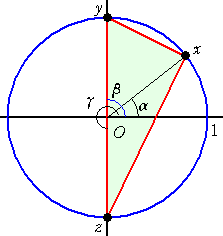このとき、題意を考えれば、ｘ、ｙ、ｚ の配置図として左図のようであるものとしてよい。
このとき、 cos(β−γ)＝ｃｏｓπ＝−１
また、余弦定理より、
ｃｏｓ(γ−α)＝−（２−（ｘ、ｙ を結ぶ線分の長さ）2）/２
同様にして、
cos(α−β)＝（２−（ｘ、ｙ を結ぶ線分の長さ）2）/２
以上から、 cos(β−γ)＋cos(γ−α)＋cos(α−β)＝−１
空舟さんが考察されました。（平成２４年３月２１日付け）
題意より、 |ｘ|=|ｙ|=|ｚ|=1 で、|ｘ+ｙ+ｚ|=1 が成り立つ。
＜複素共役を使う方法＞ 1/ｘ、1/ｙ、1/ｚ がそれぞれ ｘ、ｙ、ｚ の複素共役であることに注目
する。
A＝ｘ/ｙ+ｙ/ｚ+ｚ/ｘ を考えると、Aの実部が、cos(β-γ)+cos(γ-α)+cos(α-β) となる。
2・（Aの実部）＝A＋A~＝(ｘ/ｙ+ｙ/ｚ+ｚ/ｘ)＋(ｙ/ｘ+ｚ/ｙ+ｘ/ｚ)
＝(ｘ+ｙ+ｚ)(1/ｘ+1/ｙ+1/ｚ)-3＝|ｘ+ｙ+ｚ|2-3＝1-3＝-2
よって、 Aの実部＝cos(β-γ)+cos(γ-α)+cos(α-β)＝-1
＜ベクトルを使う方法＞ |OX+OY+OZ|＝1 の両辺を２乗して、|OX|=|OY|=|OZ|=1とすれば、
OX・OY＋OY・OZ＋OZ・OX＝-1 を得る。
このとき、 ｃｏｓα・ｃｏｓβ＋ｓｉｎα・ｓｉｎβ
＋ｃｏｓβ・ｃｏｓγ＋ｓｉｎβ・ｓｉｎγ
＋ｃｏｓγ・ｃｏｓα＋ｓｉｎγ・ｓｉｎα＝-1
すなわち、 cos(β-γ)+cos(γ-α)+cos(α-β)＝-1
（※） (ｘ+ｙ+ｚ)(1/ｘ+1/ｙ+1/ｚ) を展開するのと本質的に同じです。
この問題では、上のように |ｘ+ｙ+ｚ|=1 で十分です。ちょっと考察すれば、以下のより強い主
張ができます。
|ｘ+ｙ+ｚ|＝1 ⇔ (ｘ+ｙ)(ｙ+ｚ)(ｚ+ｘ)＝0 (ｘｙｚが三角形をなすなら、直角三角形！)
実際に、|ｘ+ｙ|≠0 ならば、|ｘ+ｙ+ｚ|＝1 かつ |ｚ|=1を満たすｚは２つしかない。
(円と円の交点で求まるから。|ｘ+ｙ|≠0 ならば、２つの円は中心が異なる。)
ｚ＝-ｘ、ｚ＝-ｙ が満たしてしまうので、他には存在しないと理解できます。
この考察をすれば、問題の等式については、２つのcosが打ち消し合い、「もう１つ＝-1」と
いう風になります。
ちなみに、ｘ+ｙ+ｚ＝ｘｙｚ となるのは、斜辺が虚軸に重なる時、すなわち、
「ｘ、ｙ、ｚ のうちどれかが ｉ、どれかが -ｉ、もう１つは任意」
の場合に限られることもわかりますね！
（コメント） 空舟さんの解はすっきりして美しいですね！最初、三平方の定理を使おうとして
計算を始めたのですが、なかなか所要の結果は得られませんでした。